• Algebra > Conic Sections

CONIC SECTIONS

Conic sections are curves that form when a plane intersects a cone at various angles. The image below shows the four conics that are formed by a plane: circle, ellipse, parabola, and hyperbola. The circle and ellipse are closed curves while the parabola and hyperbola are open.

The intersection of the plane causes 2 degenerate forms. If the plane intersects at the intersection of the lateral edges of the cone, a point is formed instead of a circle or ellipse. If the plane intersects the cone through the intersection of the lateral edges and is perpendicular to the base, it forms two lines instead of the hyperbola.

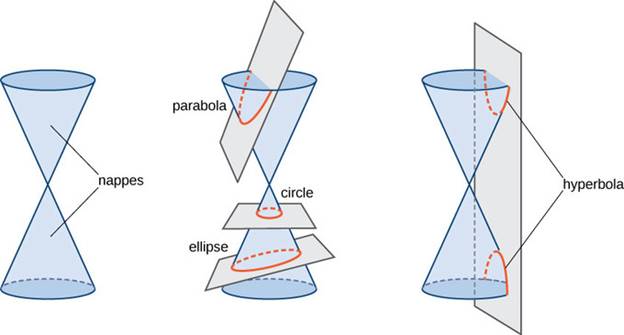
An hourglass-shaped double cone (two nappes). A horizontal plane through the cone makes a circle. A plane at an angle less than the edge of the cone makes an ellipse. A plane at the angle of the edge of the cone makes a parabola. A plane at an angle greater than the edge of the cone makes a hyperbola.

THE CIRCLE

The circle is a locus of all points that are equidistant from a point. The circle is a conic section created by slicing a cone with a plane parallel to the base of the cone. It degenerates to a point if the plane slices the cone at the intersection of the two cones.

The eccentricity of the circle is 0.

Circle D is centered at the origin and has a radius of 2. A tangent at point H is shown. It crosses the x-axis at 4 as expected. The y-intercept is 4√3/3. Circle C has its center translated to (2, 3).

For the rest of the discussion, we will assume the conic is centered at the origin, since translating the center is a matter of replacing x with x – h and y with y – k.

Tangents

Polar Form of a Circle

The polar form of a circle is simply r(θ) = a, where a is the radius of the circle. Simply, for all θ, the distance from the origin is a.

If the center of the circle is (h, k), then the polar form is: \(r(\theta) = h\cos\theta + k\sin\theta \pm\) \(\sqrt{R^2-(h\sin\theta-k\cos\theta)^2}\).

Measurements

The area of a circle of radius r is πr². The circumference, the perimeter of the circle, is 2πr. The diameter, the maximum distance between two opposite points on the circle, is 2r. The diameter is also the segment, or a chord, which passes through the center of the circle.

THE ELLIPSE

The ellipse is an oval or oblong shaped curve that is the intersection of a cone and a plane slicing the cone at an angle. The ellipse is the locus of all points such that, the sum of the point in the locus to two points, the foci, is constant.

A circle can be considered a special ellipse where a = b = r, the radius of the circle. The equation of a circle can be written as \(\dfrac{x^2}{r^2}+\dfrac{y^2}{r^2}=1\).

An ellipse has a major axis and a minor axis. If the ellipse is longer vertically, the major axis lies on the y-axis. If the ellipse is longer horizontally, the major axis lies on the x-axis.

The foci of the ellipse always fall on the major axis. In some conventions, a is assigned the bigger value and b the smaller value; therefore, a² > b². Therefore, if a² – the bigger number – is the denominator of x², then the x-axis is the major axis of the ellipse. And if a² is the denominator of y², then the y-axis is the major axis of the ellipse. On this page, we will mainly refer to a² being the denominator of x², unless otherwise noted.

The length of the major axis is 2a and minor axis is 2b. Remember that the ellipse has a constant sum. That sum is actually equal to 2a, the length of the major axis.

The distance of the foci from the center of the ellipse is c, where c² = a² – b². If the ellipse has a horizontal major axis, then the location of the foci are (c, 0) and (–c, 0). If the ellipse has a vertical major axis, then the foci are (0, c) and (0, –c).

Tangents

For simplicity, we will assume the a² term is the denominator of the x² term, irrespective of whether a or b is bigger.

This is simple to derive. The y-intercept, y_yi, is given by \(y_{yi}=y-x\dfrac{dy}{dx}\).

For the ellipse, we already know the slope of a line at point (x, y) on the ellipse is \(\dfrac{dy}{dx}=-\dfrac{b^2x}{a^2y}\). Substituting this in the y-intercept formula, we have:

(i) \(y_{yi}=y-x\dfrac{dy}{dx} = y - x\cdot-\dfrac{b^2x}{a^2y} =\) \( \dfrac{a^2y^2+b^2x^2}{a^2y} = \dfrac{a^2b^2}{a^2y} =\) \(\dfrac{b^2}{y}\)

The slope of a tangent at x = c is \(\pm\dfrac{c}{a}\), which is the eccentricity of the ellipse (discussed later). This is also true for hyperbolas.

The points at which a tangent line has a slope of 1 or –1 is \(\left( \pm\dfrac{a^2}{\sqrt{a^2+b^2}}, \pm\dfrac{b^2}{\sqrt{a^2+b^2}} \right)\).

Eccentricity of an Ellipse

The eccentricity, e, of an ellipse is greater than 0 and less than 1: 0 < e < 1. The closer e is to 0, the more the ellipse looks like a circle. When e is closer to 1, the shape of the ellipse becomes extremely oblong and starts to look more like a parabola, since the eccentricity of a parabola is 1.

Remember a > b, irrespective of whether it is the denominator of x² or y².

The directrix is a line or lines that give constant ratios with the focus. This figure allows us to find the distance of the directrix from the closest vertex of the ellipse. We know that \(e=\dfrac{c}{a}\). From the figure above, the distance from the focal point F₁ to (a, 0) and (a, 0) to the directrix must be in a ratio of e. The distance between focal point F₁ to (a, 0) is a – c. Let x be the distance from (a, 0) to the directrix. Then, \(e=\dfrac{c}{a}=\dfrac{a-c}{x}\) and \(cx=a(a-c)\). Therefore, \(x = \dfrac{a(a-c)}{c}\), and this is the distance of the directrix from (a, 0).

Now, if we want to know the distance of the directrix from the center of the ellipse to the directrix, we simply add a: \(\dfrac{a(a-c)}{c}+a=\dfrac{a^2-ac+ac}{c}=\dfrac{a^2}{c}\).

The distance of the directrix from the closest focus is \(a - c + \dfrac{a-c}{c} = \dfrac{b^2}{c}\).

Vertices of an Ellipse

The vertices of an ellipse are the points where the tangent lines are horizontal or vertical. These points are naturally (a, 0), (–a, 0), (0, b) and (0, –b). The vertices are also the 2 closest points and the 2 farthest points from the center of the ellipse.

The distance between the focus and the minor vertices is equal to a.

Polar Form of an Ellipse

This form allows us to see a and b. This ellipse is centered at the pole in the polar graph. Alternate polar forms can be written with e instead of a and b.

Above is an ellipse with the equation \( r(\theta) = \dfrac{15}{\sqrt{(3\cos\theta)^2 + (5\sin{\theta)^2}}} \). If sine has the larger coefficient, the ellipse is horizontal.

Right Angles

At which point on the ellipse does the point form a right angle with the foci? Because of symmetry, there are 4 points where this occurs, and these 4 points are actually where the circle with the same center as the ellipse and with radius of c intersects the ellipse. These 4 points are:

\(\left( \pm\dfrac{a\sqrt{c^2-b^2}}{c}, \pm\dfrac{b\sqrt{a^2-c^2}}{c} \right)\)

In the above figure, foci F and G are shown. Points A and D are the intersections of the ellipse and the circle that passes through the foci. GAF and FDG are both right triangles. Hence, AFDG is a rectangle.

The proof is quite simple. In order to form a right triangle with the foci, the right angle must fall on the circle that has a diameter passing through the foci. Where this circle intersects with the ellipse is where the right angle will be on the ellipse.

Naturally, we wonder at what points would the rectangle be a square. This occurs only in an ellipse where b = c. Hence, not all ellipse have 2 points that will form a square with the foci being the other 2 points. In this case, the x = 0. Therefore, there are only two points of intersection for the ellipse and the circle. In fact, the circle is inside the ellipse.

We can easily see, without any calculations, that b must equal c in order for ACF to be a right triangle. And hence, making GAF a right triangle because of symmetry. It should be noted that if b < c, then the circle is smaller than the ellipse and no right angle can form.

Orthogonal Tangents

If two tangents to an ellipse intersect and create a right angle, then the intersection point lies on a circle that has a radius of \(\sqrt{a^2+b^2}\). This circle is called the director circle. The proof of this and more about tangents are found here: Tangents to Ellipses.

A tangent with a slope of –1 and a tangent with a slope of 1 intersect on the y-axis. As was mentioned earlier, the point at which a tangent line has a slope of 1 or –1 is \(\left( \pm\dfrac{a^2}{\sqrt{a^2+b^2}}, \pm\dfrac{b^2}{\sqrt{a^2+b^2}} \right)\). An isosceles right triangle is created by the tangents and the x- and y-axes.

Parametric Form of an Ellipse

Both of these give an ellipse that is the same. The only difference is that starting point of the ellipse being traced as t increases. In the first case, the ellipse begins at point (a,0) and proceeds counterclockwise. In the second case, the ellipse begins at point (0, b) and proceeds counterclockwise. Whether the ellipse is horizontal or vertical depends on whether a or b is bigger.

The slope of the tangent at t is given by \(\dfrac{dy}{dx} = -\dfrac{b}{a}\cot(t)\) for the first case and \(\dfrac{dy}{dy} = -\dfrac{b}{a}\tan(t)\) for the second case.

Measurements

The area of an ellipse is abπ. The circumference of an ellipse can only be approximated. There is no closed form for the circumference.

The function form of the ellipse is \(f(x) = \pm\dfrac{b}{a}\sqrt{a^2-x^2}\). Since the complete ellipse cannot be written as a function, we can split it as the plus and minus for the top and bottom portion of the ellipse to graph is completely.

This form also allows us to calculate partial areas of the ellipse. In the integral, we let \(x=a\sin(t)\) so that \(dx=a\cos(t)dt\).

(i) \(\displaystyle \int \dfrac{b}{a}\sqrt{a^2-x^2} dx = \) \(\dfrac{b}{a} \displaystyle \int \sqrt{a^2-a^2\cos(t)^2}\cdot a\cos(t)dt =\) \(\dfrac{ab}{2} \displaystyle \int 1+\cos(2t) dt = \dfrac{ab}{2}\left [t+\dfrac{\sin(2t)}{2} \right]\)

Substituting back \(t=\arcsin\dfrac{x}{a}\), we get

(ii) \(\dfrac{ab}{2}\left[\arcsin\dfrac{x}{a}+\dfrac{\sin(2\arcsin\dfrac{x}{a})}{2} \right ]\)

Applying the limits 0 and a, gives us:

(iii) \(\dfrac{ab}{2}\left[\arcsin 1+\dfrac{\sin(2\arcsin 1)}{2} \right ] - \) \( \dfrac{ab}{2}\left[\arcsin 0+\dfrac{\sin(2\arcsin 0)}{2} \right ] = \dfrac{ab\pi}{4}\)

In the polar form, we can measure the area of a sector swept out by an angle from angle a to b. The area in polar form is \(A=\dfrac{1}{2}\int_{a}^{b}r(\theta )d\theta\). For the ellipse, this is:

(i) \(A=\dfrac{(ab)^2}{2} \displaystyle \int \dfrac{1}{(b\cos\theta)^2+(a\sin\theta)^2} d\theta = \) \(\dfrac{(ab)^2}{2}\cdot \dfrac{\arctan \dfrac{b\tan\theta}{a}}{ab}=\dfrac{ab}{2}\cdot\arctan\dfrac{b\tan\theta}{a}\)

If we assume the inverse tangent of infinity is π/2, then the area of the sector from 0 to π/2 is:

(ii) \(A = \left [ \dfrac{ab}{2}\cdot\arctan\dfrac{b\tan\theta}{a} \right ]^\dfrac{\pi}{2}_{0} = \) \( \dfrac{ab}{2}\cdot\arctan\dfrac{b\tan\dfrac{\pi}{2}}{a} - \dfrac{ab}{2}\cdot\arctan\dfrac{b\tan(0)}{a} =\) \(\dfrac{ab}{2}\arctan(\infty ) = \dfrac{ab}{2}\cdot\dfrac{\pi}{2} = \dfrac{ab\pi}{4}\)

We expected the sector would be quarter of the area of the whole ellipse.

THE HYPERBOLA

The hyperbola is a curve formed by a plane intersecting a cone perpendicularly to the base of the cone. If the place intersects at tip of the cone, it degenerates into two intersecting lines.

Similar to an ellipse, which has a constant sum with respect to the foci, a hyperbola is a curve of constant difference with respect to the foci.

In the above image, The foci of the hyperbola are F₁ and F ₂. The image shows the lengths a, b, and c. AF₁ is c. A segment tangent to (c, 0), the vertex, and intersecting the asymptotes is equal to 2b. The length a is the distance from the center to the vertex. The hyperbola is symmetric so this applies to the branch on the negative x-axis also.

The difference GD – DF is a fixed constant. Therefore, FE – EG would be equal to GD – DF. The hyperbola is also defined by the eccentricity, which involves the directrix. The eccentricity of the hyperbola is greater than 1. In the above image, FD/DH = GE/EI = e, where e > 1.

The hyperbola has two asymptotes, pictured in red above.

The distance AF is defined as c and AC is defined as a. In contrast to the ellipse, for a hyperbola, a² + b² = c². Therefore, \(b = \sqrt{c^2 - a^2}\).

In the first case where y term is negative, the hyperbola has its foci on the x-axis. If the x term is negative, the foci will be on the y-axis and will be oriented up and down.

Tangents

The slope of a tangent at x = c is \(\pm\dfrac{c}{a}\), which is the eccentricity of the hyperbola (discussed later). This is also true for ellipses.

The point at which a tangent line has a slope of 1 or –1 is \(\left( \pm\dfrac{a^2}{\sqrt{a^2+b^2}}, \pm\dfrac{b^2}{\sqrt{a^2+b^2}} \right)\).

Polar Form of a Hyperbola

This hyperbola is centered at the pole in the polar graph. If the hyperbola opens up and down instead, its equation would be \(r(\theta) = \dfrac{ab}{\sqrt{(b\sin\theta)^2 - (a\cos{\theta)^2}}}\). Alternate polar forms can be written with e instead of a and b.

In the graph above, a and b were switched to show that the hyperbola changes orientation.

Parametric Form of a Hyperbola

Both of these give a hyperbola. The first gives a hyperbola that opens left and right. The latter opens up and down.

The slope of the tangent at t is given by \(\dfrac{dy}{dx}=\dfrac{b}{a}\coth(t)\) for the first case. In the second case, the slope is \(\dfrac{dy}{dx} = \dfrac{b}{a}\tanh(t)\).

Alternatively, the parametric equation of a hyperbola can be written using trigonometric functions instead of hyperbolic (i.e. exponential) functions. Remember that \(\cos^2x + \sin^2x = 1\) and sine and cosine can be used to define the circle and ellipse. In the same way, \(\cosh^2x - \sinh^2x = 1\) and the hyperbolic counterparts define a hyperbola. In the same way, the trigonometric identities that always give a different of 1 are secant and tangent: \(\sec^2x - \tan^2x = 1\).

Again, the first opens left and right, while latter opens up and down. In the first case, the slope of a line at t is given by \(\dfrac{dy}{dx} = \dfrac{b}{a}\csc(t)\). In the second case, the slope is give by \(\dfrac{dy}{dx} = \dfrac{b}{a}\sin(t)\)

There is a difference in the hyperbolic and trigonometric parametric equations of the hyperbola. In the hyperbolic version, only one branch of the hyperbola is traced unless one uses \(\pm\cosh(t)\). Since cosh(t) will never be negative for any t, only one brance (the branch on the positive x-axis) is traced. When one takes the negative of cosh(t), then the branch on the negative x-axis is traced.

This is not an issue with the trigonometric form since the range of tan(t) and sec(t) includes all numbers for the domain –π < t < π.

THE PARABOLA

The parabola is a conic section formed from the intersection of a plane and a cone where the plane is parallel to the lateral edge of the cone.

The parabola has one focus and one directrix. It is different from the rest because it has only one squared term. If the parabola opens up or down, it can be represented by a function.

The parabola has interesting properties of its own.

First, by definition, the ratio of the distance between the point on the parabola to the focus and the distance between that point and the directrix is 1. In the image above, FP/PD = 1.

The parabola has the equation y = ax² if it opens upward. It is an even function and has line symmetry about the y-axis. The focus is located on the line of symmetry at (0, 1/(4a)). The directrix is also 1/(4a)) units from the vertex of the parabola.

In the figure above, a tangent to point P intersects the y-axis at C. Segment PD is perpendicular to the directrix. The segment FC is always equal to PD. A segment FD intersects the x-intercept at E which is also the x-intersect of the tangent at P. Since PD = FP (by definition of a parabola), the quadrilateral FPDC is a rhombus. Its diagonals form a right angle.

Orthogonal Tangents

If a tangent to a parabola is at (p, ap²), then its orthogonal tangent, the tangent that mades a 90° angle at their intersection, is at \(\left (-\dfrac{1}{4a^2p},\dfrac{1}{16a^3p^{2}}\right)\).

The Geogebra activity allows you to drag point P and see how a tangent at point B makes a right angle with the tangent at point P. You can also change a to any value. (For mobile devices, you may need to adjust the sketch to bring it into view. Or you can view the activity in full screen to view the whole graph.)

To read more about interesting properties of parabolas, see this page: Properties of Parabolas.

ECCENTRICITY

The eccentricity can be thought of as: to what degree does a conic deviates from a circle which as an eccentricity of 0? The closest conic to a circle is the ellipse. The eccentricity, e, of an ellipse is greater than 0 and less than 1: 0 < e < 1. The closer e is to 0, the more it looks like a circle. As e approaches 1, the ellipse looks less and less like a circle and more and more like a parabola. The eccentricity of a parabola is 1. For hyperbolas, the eccentricity is greater than 1.

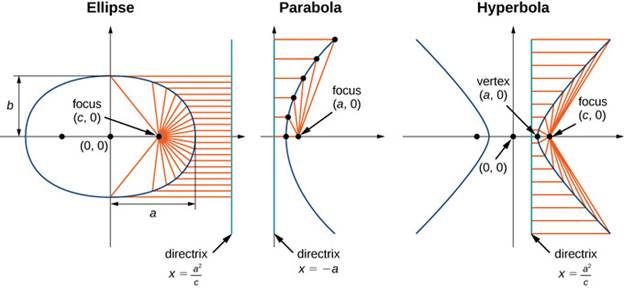
A directrix is a line used to construct and define a conic section. The ratio of the distance between a point on the directrix and a point on the conic section to the distance between that point on the conic section to the focus is contant ((i.e. the eccentricity). A parabola has one directrix, while ellipses and hyperbolas have two. A circle does not have a directrix.

The easier way to determine the equation of a conic in terms of e is to derive the equation in polar form.

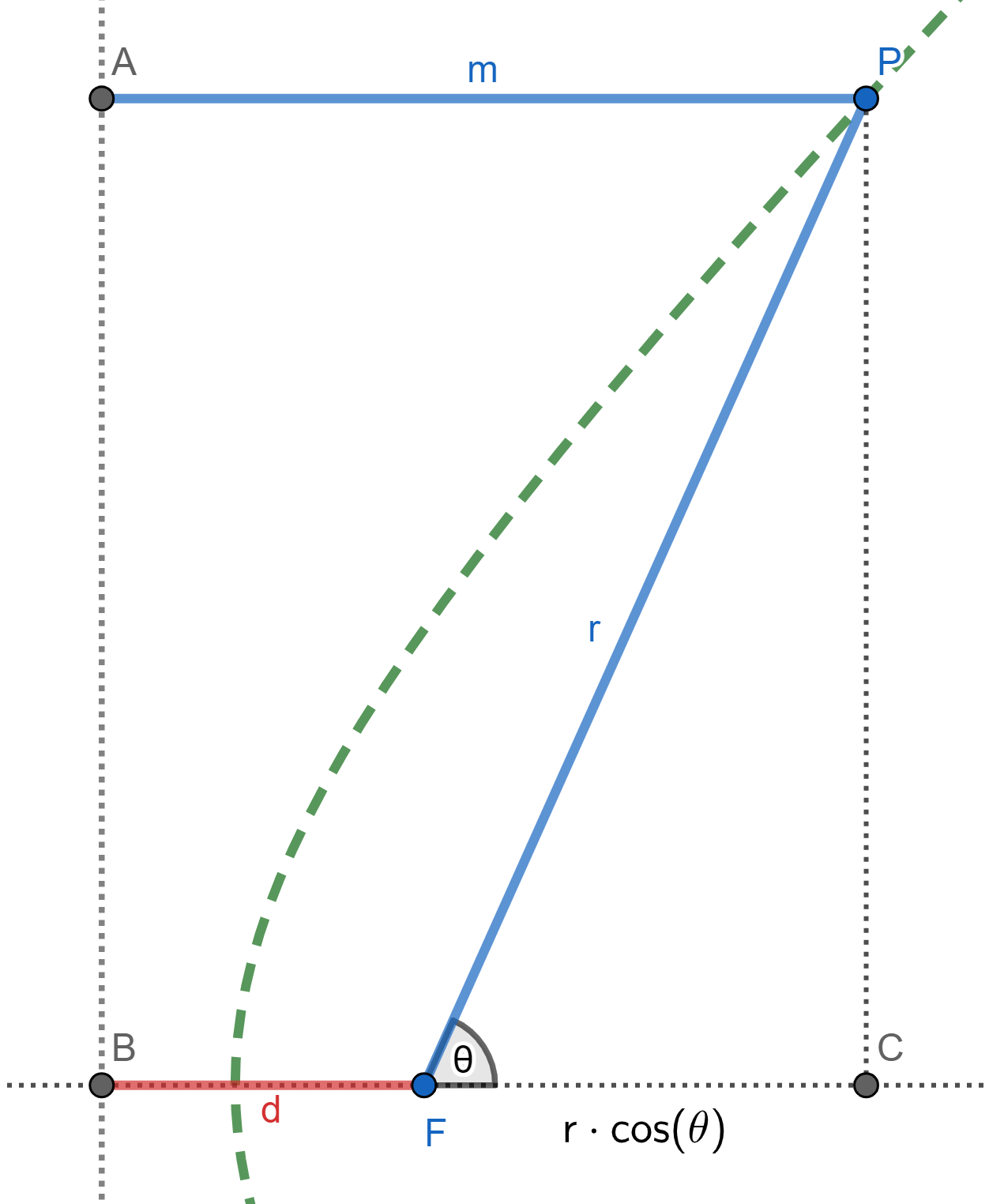
In the image above, F is the focus point at the pole. It is d units away from the directrix, which is the line containing segment AB. By definition of eccentricity, \(e=\dfrac{r}{m}\) or \(r = em\). The length of AP, m, is simply equal to BC, which is equal to \(d + r\cdot\cos\theta\). Therefore, \(r = e(d+r\cdot\cos\theta)\). We solve for r and write it in terms of θ for the final equations.

From the standard form of conics, we can determine the eccentricity from a, b, and c.

The eccentricity of an ellipse is given by \(e=\dfrac{\sqrt{a^2-b^2}}{a}= \dfrac{c}{a}\) where a > b. (Remember a > b, irrespective of whether it is the denominator of x² or y².

For a hyperbola, the eccentricity is \(e=\dfrac{\sqrt{a^2+b^2}}{a}= \dfrac{c}{a}\). Although the formula is the same for both the ellipse and hyperbola, the values differ because e is > 1 for a hyperbola and 0 < e < 1 for an ellipse.

The ellipse and hyperbola both have two directrices. The parabola has one.

We can convert this polar form into the standard form by substituting \(r^2=x^2+y^2\) and \(\cos\theta = \dfrac{x}{r}\). We can write this in two ways. First way is for parabolas before we divide to get the standard form of the ellipse and hyperbola: \((1-e^2)x^2 + y^2 - (2e^2d)x = (ed)^2\). We let e = 1 so the equation becomes the following:

This form is better for parabolas because when e = 1, the x² term is 0 and the parabola opens left or right as we would expct. So the equation for a parabola is essentially: \(y^2 - (2d)x = d^2\) where d is distance from the focus to the directrix.

For ellipses, and hyperbolas, we can take the previous equation, complete the squares, and obtain the standard form:

In this form, we can see why completing the square does not result in an equation suitable for parabolas.

Because we derived the equation of the conics where the focus was at the origin, note that these equations give conics with the focus at the origin, not the center of the conic.

When e = 0, we get a degenerate form instead of the equation for a circle. That was expected since the orignal polar form does not work for circles, which has a simple equation r(θ) = a, where a is the radius of the circle.

THE REFLECTIVE PROPERTY OF CONICS

The Circle and Ellipse

Conics have reflective properties that can be interesting. The circle, for example, has a simple reflective property that requires no proof to visualize. If a ray passes through the center of the circle from the inside, it will reflect back to the center. Alternatively, if a ray is aimed at the center of the circle, it will reflect back straight to the source.

Ellipses have a reflective property where a ray passing through one focus will reflect on the perimeter of the ellipse and pass through the second focus. In the image, a billard ball shot through F₁ will bounce off at point P on the ellipse and pass through F₂. Note that if a ray is aimed at one focus externally, than it will reflect off in a line that is continuous with the other focus. If one proves the first case, by virtue of vertical angles being equal, the second case is easily proved.

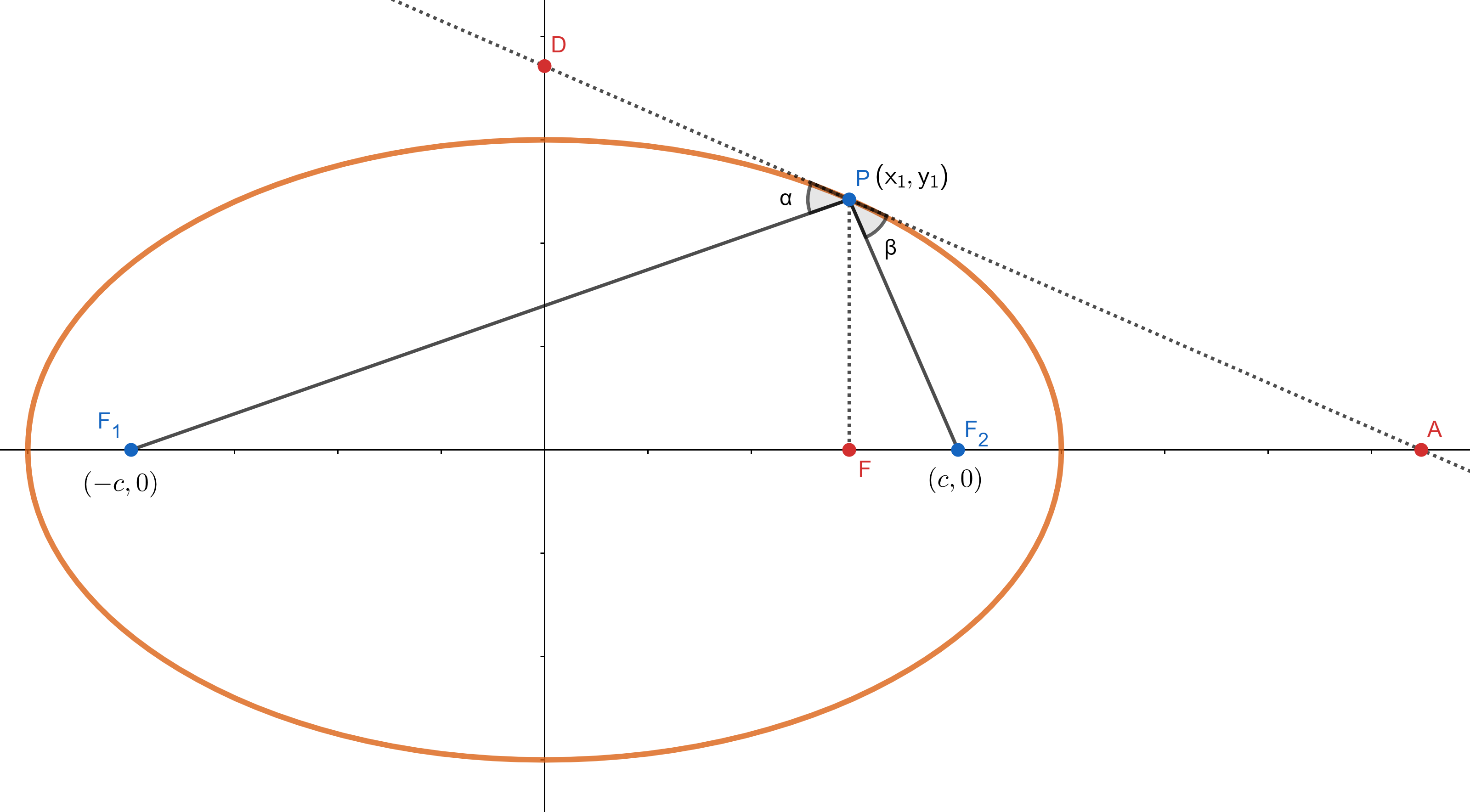
In order to prove the first case, we need to prove that angles α and β are equal. It is known that the angle between two lines is given by \(\theta = \arctan\left(\dfrac{m_{1}-m_{2}}{1+m_{1}m_{2}}\right)\), where m₁ and m₂ are the slopes of the two lines. We will use this equation to determine that the angles are equal.

First, note that if the quantity \(\dfrac{m_{1}-m_{2}}{1+m_{1}m_{2}}\) is the same for the angle between F₁P and PD and angle between F₂P and PA, then the arctangents will be equal. We simply have to prove this equality for both angles.

From the section on ellipses, the slope of a tangent at (x, y) is given by \(m = -\dfrac{b^2x}{a^2y}\).

The slope, m₁, of F₁P is \(m_{1} = \dfrac{y}{x+c}\) by simply taking the difference in y values and x values.

Similarly, the slope, m₂, of F₂P is \(m_{2} = \dfrac{y}{x-c}\).

The quantity \(\dfrac{m_{1}-m_{2}}{1+m_{1}m_{2}}\) for the first pair is \(\dfrac{\dfrac{y}{x+c}+\dfrac{b^2x}{a^2y}}{1-\dfrac{y}{x+c}\cdot\dfrac{b^2x}{a^2y}} = \) \( \dfrac{\dfrac{b^2cx+a^2b^2}{a^2y(x+c)}}{\dfrac{y[(a^2-b^2)x+a^2c]}{a^2y(x+c)}} =\) \(\dfrac{b^2(cx+a^2)}{cy(cx+a^2)} =\dfrac{b^2}{cy}\).

For the second pair, this is \(\dfrac{\dfrac{y}{x-c}+\dfrac{b^2x}{a^2y}}{1-\dfrac{y}{x-c}\cdot\dfrac{b^2x}{a^2y}} = \) \( \dfrac{\dfrac{-b^2cx+a^2b^2}{a^2y(x-c)}}{\dfrac{y[(a^2-b^2)x-a^2c]}{a^2y(x-c)}} =\) \(\dfrac{-b^2(cx-a^2)}{cy(cx-a^2)} = -\dfrac{b^2}{cy}\).

We obtained a negative value for the second pair because of the order in which we took the slopes, meaning that the line F₂P is greater than 90° and has a negative slope. However, once we use the absolute values of the angle, we get the same arctangent value. Therefore, the angles α and β are equal.

The Parabola

In a parabola, a ray passing through the focus will reflect off the parabola perpendicular to the directrix. The image below offers a visual proof once you realize FPDC is a rhombus.

When we extend line DP, which is perpendicular to the directrix, we must prove the angles β and δ are equal. Since FPDC is a rhombus, angles β and γ are equal. Hence, angles γ and δ are equal, and so all three angles are equal, in fact.

The Hyperbola

The hyperbola has the same reflective property as the ellipse. A ray aimed at one focus will reflect and travel toward the second focus. A ray aimed toward the focus externally will not actually touch either foci. And a ray aimed internally will touch one focus but not the other. However, their line of travel will cross the focus.

ROTATON OF CONICS

Initially when I started writing this part, it wasn’t as lengthy and my goal was to define the standard equation of conics based on the coefficients of the rotated conic. Basically, turn the equation \(A'x^2 + B'xy + C'y^2 + D'x + E'y + F' = 0\) into \(Ax^2 + Cy^2 + Dx + Ey + F = 0\), where A, C, D, E, and F are defined in terms of A', B', C', D', E', and F'.

In eliminating the trigonometry, I came up with somewhat simple equations for the coefficients of the standard conic that worked for the examples that I had used - coincidentally! But on using it with more examples, I found 2 cases where the equations failed.

(1) The equations for the coefficients failed when the angle of rotation was negative. I reinvestigated the trigonometric calculations that led to the coefficient equations and made changes to account for the negative angle of rotation.

(2) The equations failed when A' was less than C'. This again made me look closely at the trigonometric calculations that led to the coefficients, and I realized the problem and corrected the shortcomings.

Adding all the explanation of “why” for all the changes, this section became long enough for its own page. I must say going in, I did not have as much clarity of rotation angles and rotation of axes as I do now.

Please see this page for all about rotation of conics: Rotation of Conic Sections.

Anirdesh.com