• Trigonometry > Constant Product Curve

Constant Product Curve

Problem: Find a locus of all points such that the product of the distances from a point in the locus to two fixed points is constant.

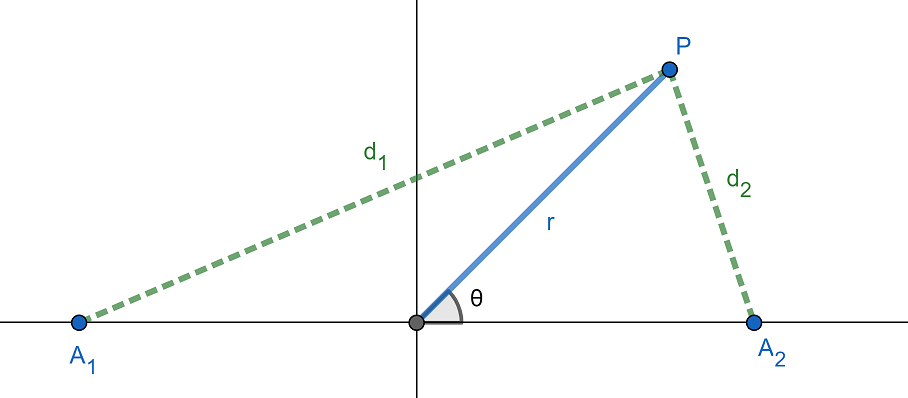
The problem is made simple if we find the locus in terms of polar coordinate system and assign the two points the coordinates A₁(–a, 0) and A₂(a, 0) as done in Figure 1. We let the product equal P and the distance between A₁ and P be d₁ and A₂ and P be d₂ so that d₁d₂ = P. Therefore, we have to express r in terms of θ. Using the Law of Cosines, we have the following equalities:

(i) $d_{1}^{2} = a^2 + r^2 - 2 \left|a\right|r\cos(\pi-\theta) = $ $a^2+r^2+2\left|a\right|r\cos\theta$

(ii) $d_{2}^{2} = a^2 + r^2 - 2 \left|a\right|r\cos(\theta) = $ $a^2+r^2-2\left|a\right|r\cos\theta$

Multiplying (i) and (ii), we obtain:

(iii) $d_{1}^{2}d_{2}^{2} = P^2 =$ $ (a^2+r^2+2\left|a\right|r\cos\theta)(a^2+r^2-2\left|a\right|r\cos\theta)=$ $(a^2+r^2)^2-4a^2r^2\cos^2\theta$

Simplifying (iii) leads to:

(iv) $P^2 = r^4+a^4-2a^2r^2(2\cos^2\theta-1) =$ $r^4+a^4-2a^2r^2\cos(2\theta)$

Solving for r², we obtain the polar form as:

(v) $r^2 = a^2\cos(2\theta) \pm \sqrt{P^2-a^4\sin^2(2\theta)}$

Lemniscate

An interesting case occurs when the product P equals a₂. The equation reduces to that of a Lemniscate.

(v) $r = \pm \sqrt{a^2\cos(2\theta) \pm a^2\sqrt{1-\sin^2(2\theta)}} = $ $\pm a\sqrt{2\cos(2\theta)}$

The rectangular form of the lemniscate is $(x^2+y^2)^2 = 2a^2(x^2-y^2)$. If we solve for a, we get $a = \frac{x^2+y^2}{\sqrt{2(x^2-y^2)}}$.

The Geogebra activity below shows a lemniscate for a = 2. You can drag the point around to see the lengths change and the product remains constant.

Anirdesh.com