Maximum Length of a Ladder Problem

Problem: Find the maximum length, L_max, of a ladder that can pass through a hall of width of w₁ to a hall of width w₂ if the ladder is carried exactly parallel to the floor.

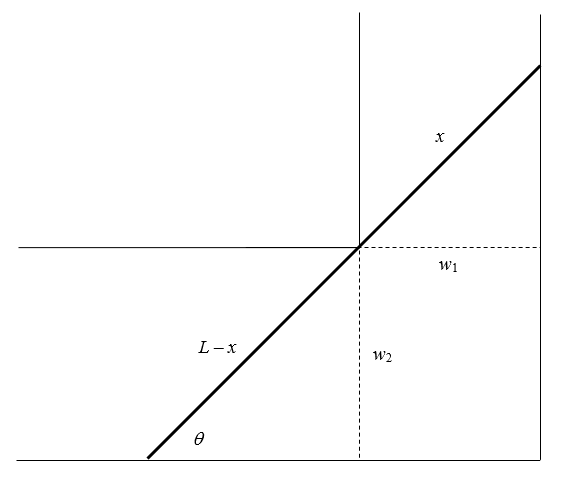
Let us consider the length, L, of the ladder as a function of θ, the angle which it makes with respect to one of the walls of the hall as shown in Figure 1. We have the following equalities from the figure:

(1) \( \cos\theta = \frac{w_1}{x}\)

(2) \( \sin\theta = \frac{w_2}{L-x} \)

Solving for x in (i) and substitution into (ii) gives:

(i) \( L = \frac{w_1}{\cos\theta} + \frac{w_2}{\sin\theta} \)

To find maximum of L, we take the derivative of L with respect to θ and set the derivative to 0 to solve the value of θ that will maximize L.

(ii) \( \frac{dL}{d\theta} = w_1\frac{\sin\theta}{\cos^2\theta} - w_2\frac{\cos\theta}{\sin^2\theta} = 0 \)

(iii) \( w_1\sin^3\theta - w_2\cos^3\theta = 0 \)

(iv) \( \tan^3\theta = \frac{w_2}{w_1} \)

Therefore, the angle that maximizes L is \( \theta = \arctan\sqrt[3]{\frac{w_2}{w_1}} \) . To find the maximum length of the ladder, we substitute this value into (i).

(v) \( L = \frac{w_1}{\cos\left(\arctan\sqrt[3]{\frac{w_2}{w_1}}\right)} + \frac{w_2}{\sin\left(\arctan\sqrt[3]{\frac{w_2}{w_1}}\right)} \)

We can use a right triangle with sides of \( w_1^{\frac{1}{3}} \) and \( w_2^{\frac{1}{3}} \) to find the sine and cosine of this angle.

(vi) \( \sin\left(\arctan\sqrt[3]{\frac{w_{2}}{w_{1}}}\right) = \frac{w_{2}^{\frac{1}{3}}}{\left(w_{1}^{\frac{2}{3}} + w_{2}^{\frac{2}{3}}\right)^{1/2}} \)

(vii) \( \cos\left(\arctan\sqrt[3]{\frac{w_{2}}{w_{1}}}\right) = \frac{w_{1}^{\frac{1}{3}}}{\left(w_{1}^{\frac{2}{3}} + w_{2}^{\frac{2}{3}}\right)^{1/2}} \)

Substituting (vi) and (vii) into (i), we get:

(viii) \( L = \dfrac{w_1}{\frac{w_1^{\frac{1}{3}}}{\left(w_1^{\frac{2}{3}} + w_2^{\frac{2}{3}}\right)^{1/2}}} + \dfrac{w_2}{\frac{w_2^{\frac{1}{3}}}{\left(w_1^{\frac{2}{3}} + w_2^{\frac{2}{3}}\right)^{1/2}}} \)

(ix) \( L = \left(w_1^{\frac{2}{3}} + w_2^{\frac{2}{3}}\right)^{1/2}\cdot w_1^{\frac{2}{3}} + \left(w_1^{\frac{2}{3}} + w_2^{\frac{2}{3}}\right)^{1/2}\cdot w_2^{\frac{2}{3}} \)

(x) \( L = \left(w_1^{\frac{2}{3}} + w_2^{\frac{2}{3}}\right)^{1/2}\cdot\left(w_1^{\frac{2}{3}} + w_2^{\frac{2}{3}}\right) \)

(x) \( L = \left(w_1^{\frac{2}{3}} + w_2^{\frac{2}{3}}\right)^{3/2} \)

Therefore, our maximum length of the ladder is \( L_{\text{max}} = \left( w_{1}^{2/3} + w_{2}^{2/3} \right)^{3/2} \) .

Observations

If the hallways are equal in width, then we have \( L_{\text{max}} = \left( 2\cdot w^{2/3}\right)^{3/2} = 2\sqrt{2}w \) and the angle that corresponds to this ladder size is 45°.

Of course, if the ladder is carried at some angle with respect to the floor instead of parallel, it could be longer. That is a problem in itself.

Example

Suppose the width of the halls are 3 and 2. Then the maximum ladder length is \( \left( 2^{2/3} + 3^{2/3} \right)^{3/2} \approx 7.02 \). The angle that corresponds to this ladder length is \( \theta = \arctan\sqrt[3]{\frac{3}{2}} \approx 41.14^{\circ} \) and the complementary angle is 48.96°.

In the Geogebra activity above, move the point P up and down to simulate the length of the ladder. You can get close to the angle 41.14° and see that this is the point which gives the minimum length, which would be the maximum length of the ladder.

Change the location of the corner, which is located at (P₁, P₂) to change the width of the halls.