Triangle Properties

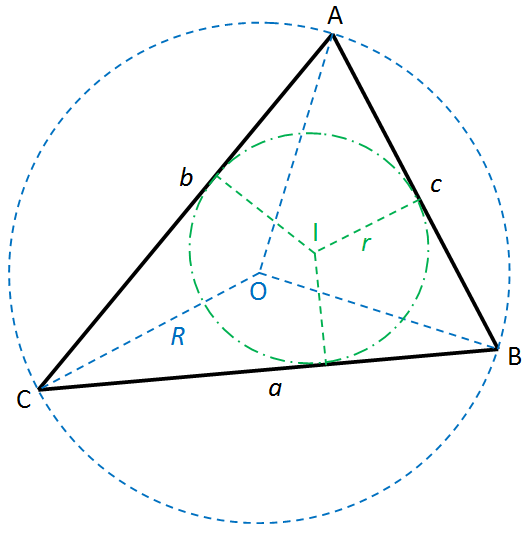
I have collected some properties related to triangles on this page. It will provide a reference to some useful formulas. On this page, the verticies of the triangle will be referred to as A, B, and C, and the length of the sides opposite to these vertices will be a, b, and c, respectively. Refer to image on right for the properties below.

The circumcircle is a circle that passes through the 3 vertices of a triangle. The circumradius, R, of a triangle is the radius of the circumcircle. The length is given by the formula: \(R=\frac{abc}{4K}\), where K is the area of the triangle.
The center of the circumcircle, O, is the point of concurrency of the perpendicular bisectors of the triangle.
The inradius, r, of a triangle is the radius of the circle which is tangent to all of its sides. The length is given by the formula: \(r=\frac{2K}{P} = \frac{K}{S}\), where P is the perimeter of the triangle.
For any triangle with sides a, b, and c, the area of the triangle is given by the formula: \(K=\sqrt{S(S-a)(S-b)(S-c)}\).

Law of Sines

The Law of Sines are relations between the angles of the vertices and the opposite sides of the triangle. The ratios of sines of the angles to the opposite sides are equivalent for all three angle/side pairs. The relationship is: \(\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}\).

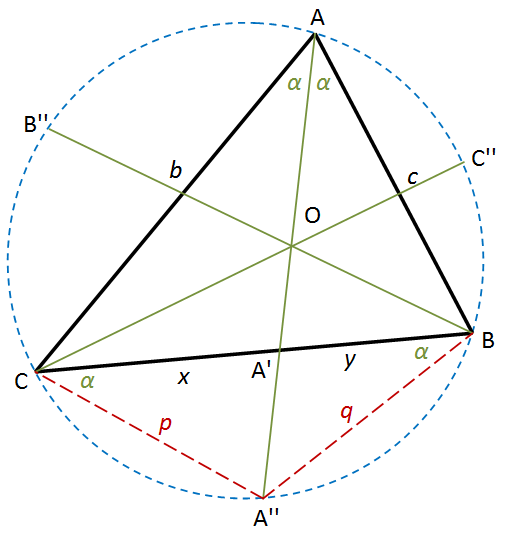
The proof is quite easy. We extend the radius from side B to meet the circle at B'. The length of BB' is 2R. Then we connect CB'. The measure of ∠CB'B is equal to A. Therefore, \(\sin{A}=\frac{a}{2R}\). We can derive similar relationships for the other two sides. Solving for 2R, we find that these relationships are all equal, giving us the law of sines:

Law of Sines. In a triangle, the ratios of the sines of an angle to its sides are all equivalent: \(\dfrac{\sin{A}}{a} = \dfrac{\sin{B}}{b} = \dfrac{\sin{C}}{c}\).

Law of Cosines

The Law of Cosines are another important set of relationships that allow us to find the measure of a third side when two sides and an included angle are known.

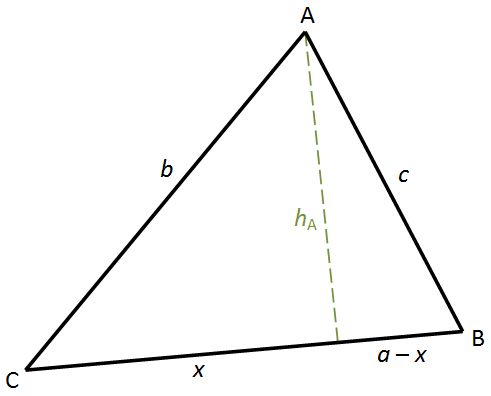
Deriving the Law of Cosines is fairly simple. In the figure on the right, we draw the altitude h_A from vertex A to side a. Let x and a - x be how it divides side a. The Pythagorean Theorem gives us \(x^2+h_{\text{A}}^{2}=b^2\) and \((a-x)^2+h_{\text{A}}^{2}=c^2\). Also, \(\cos{C}=\frac{x}{b}\). Solving for \(h_{\text{A}}^{2}\) and equating the two gives us the Law of Cosines.

Law of Cosines. In a triangle, the following relationship between two sides and the included angle is true: \(c^2=a^2+b^2-2ab\cos{C}\).

When C = 90°, cos C = 0. The formula reduces to the famous Pythagorean theorem c² = a² + b². The relationships for the other 2 sides can be derived similarly.

Cevians

Cevians are lines drawn from a vertex to the opposite side of a triangle. There are 3 special cevians: medians, altitudes, and angle bisectors. Cevians are concurrent if and only if they satisfy a certain condition which was stated by Ceva. The condition and proof are given here: Ceva’s Theorem.

Medians, altitudes, and angle bisectors are all cevians that are concurrent.

Angle Bisectors

An angle bisector from a vertex divides the opposite side into ratio equal to the ratio of the two other sides. In the figure on the left, x/y = b/c = x/(a – x). The proof is quite easy. Triangle ΔACA' is similar to triangle ΔAA''B. Hence, \(\frac{b}{x}=\frac{\text{AA}''}{q}\). Similarly, \(\frac{c}{y}=\frac{\text{AA}''}{p}\). Also note that p = q because they are the chords of equal angles, α. Hence, \(\frac{b}{x}=\frac{c}{y}\) or \(\frac{b}{c}=\frac{x}{y}\). Since p = q, ΔCA''B is an isosceles triangle.

By Ceva’s theorem, the angle bisectors are concurrent at a common point: \(\frac{\text{CA}'}{\text{A}'\text{B}}\cdot \frac{\text{BC}'}{\text{C}'\text{A}}\cdot \frac{\text{AB}'}{\text{B}'\text{C}}\) = \(\frac{b}{c}\cdot \frac{a}{b}\cdot \frac{c}{a} = 1\).

The lengths of the angle bisectors are given by:

\(\text{AA}' = \frac{2bc\cdot \cos \alpha }{b+c}\), \(\text{BB}' = \frac{2ac \cdot \cos \beta }{a+c}\), and \(\text{CC}' = \frac{2ab\cdot \cos \gamma }{a+b}\), where AA', BB', and CC' are the angle bisectors from vertex A, B, and C, respectively.

The angle bisectors divide the opposite side as follows: \(\text{CA}' = x = \frac{ab}{b+c}\) and \(\text{BA}' = a-x = \frac{ac}{b+c}\).

The lengths of ΔA'B'C' can be determined using the Law of Cosines. The length of side A'B' is given by: \(\text{A}'\text{B}' = \frac{ab\sqrt{{c^2}+2cP(1-\cos \gamma )}}{(a+c)(b+c)} =\) \(\frac{\sqrt{{(abc)^2}+abcP[{{c}^{2}}-(a-b)^2]}}{(a+c)(b+c)}\), where P is the perimeter of the triangle. The length of the other sides can be found similarly.

Altitudes

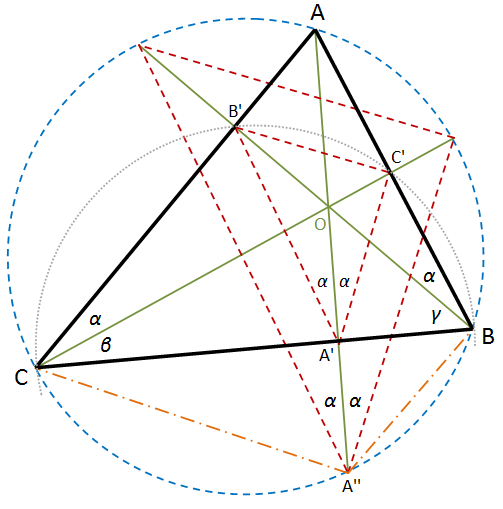
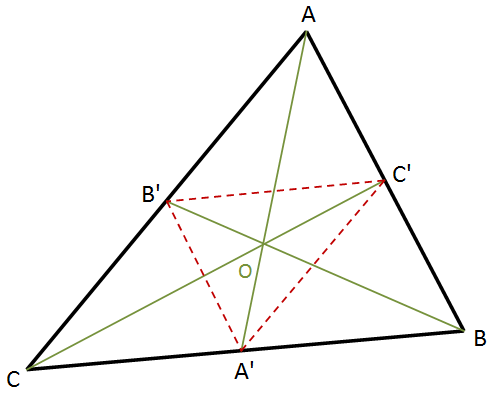
The altitudes of a triangle are concurrent at a common point, O. Proof is shown below.

Triangle pairs ΔCB'B and ΔCC'B, pair ΔBA'A and ΔBB'A, and pair ΔAA'C and ΔAC'C are all right triangles that have a common circumscribed circle with the diameter of the circle being their common side. Part of the common circumcircle of triangles ΔCB'B and ΔCC'B is shown.
The length of the altitudes in terms of the sides of the triangle can be found by noting that the altitudes can be used to find the area of the triangle. The area of the triangle in turn can be expressed in terms of the sides by Heron’s formula.
The vertices of ΔABC are the centers of the excircles of ΔA'B'C'.
The altitudes of ΔABC are the angle bisectors of ΔA'B'C'. Triangle ΔA'B'C' is called the orthic triangle.
Since quadrilaterals AC'A'C, BA'B'A, and CB'C'B are all cyclic, the lengths of the sides of the orthic triangle can be determined: \(\text{B}'\text{C}' = \frac{h_{\text{B}}\cdot h_{\text{C}} - \sqrt{(a^2-h_{\text{B}}^2)({a^2}-h_{\text{C}}^2)}}{a}\), \(\text{A}'\text{C}' = \frac{h_{\text{A}}\cdot h_{\text{C}} - \sqrt{(b^2-h_{\text{A}}^2)(b^2-h_{\text{C}}^2)}}{b}\), and \(\text{A}'\text{B}' = \frac{h_{\text{A}}\cdot h_{\text{B}} - \sqrt{(c^2-h_{\text{A}}^2)(b^2-h_{\text{B}}^2)}}{c}\), where h_A, h_B, and h_C are the altitudes to sides A, B, and C, respectively.
The altitudes were extended to meet the circumscribed circle of triangle ΔABC. The resulting triangle has sides parallel to the orthic triangle and is similar to the orthic triangle.
CO = CA'' and BO=BA''. BOA'' and COA'' are both isosceles triangles. This can easily be observed from the fact that β = 90° - B° and CA''A = B°.

Proof of concurrency. The triangle pair ΔB'OC and ΔBOC', the pair ΔA'OB and ΔAOB', and the pair ΔAOC' and ΔA'OC are similar triangles by SAA property. Using Ceva’s theorem, the altitudes are concurrent: \(\frac{\text{CA}'}{\text{A}'\text{B}}\cdot \frac{\text{BC}'}{\text{C}'\text{A}}\cdot \frac{\text{AB}'}{\text{B}'\text{C}} =\) \(\frac{\text{CA}'}{\text{C}'\text{A}}\cdot \frac{\text{BC}'}{\text{B}'\text{C}}\cdot \frac{\text{AB}'}{\text{A}'\text{B}} =\) \(\frac{\text{OA}'}{\text{OC}'}\cdot \frac{\text{OC}'}{\text{OB}'}\cdot \frac{\text{OB}'}{\text{OA}'} = 1\).

Medians

Median are cevians that divide the opposite side into equal lengths. It is easy to determine that the medians are concurrent by using Ceva’s Theorem. The point of concurrency of the medians is the center of gravity of the triangle. As a matter of fact, any segment that passes through the point of concurrency will divide the triangle into equal areas.

The medial triangle has sides parallel to the original triangle.
AB'A'C', BA'B'C', and CB'C'A' are all parallelograms.
The medians divide each other in a ratio of 2:1. Therefore, AO = 2(AA')/3.
The medial triangle is similar to triangle ABC with its sides half the length of ABC. The medial triangle of the medial triangle is similar to both triangles.
The medians form six triangles of equal area.
The length of the medians of a triangle in terms of its sides are given by: \(\text{AA}' = m_{\text{A}} = \frac{\sqrt{2b^2+2c^2-a^2}}{2}\), \(\text{BB}' = m_{\text{B}} = \frac{\sqrt{2a^2+2c^2-b^2}}{2}\), and \(\text{CC }' = m_{\text{C}} = \frac{\sqrt{2a^2+2b^2-c^2}}{2}\).

Perpendicular Medians

If the medians are perpendicular, then we discover many interesting relationships, especially if the triangle is isosceles.

If the median from vertex A and vertex B are perpendicular, then \(a^2 + b^2 = 5c^2\). The proof is quite simple.

The right triangle AOB' gives us the following relationship: \(a'^2+b''^2 = \left(\frac{b}{2}\right)^2\). The right triangle AOB gives us the relationship: \(a'^2 + b'^2 = c^2\). We solve for \(a'\) and substitute that into the second equation to obtain: \(b'^2+\frac{b^2}{4}-b''^2=c^2\).

Note that \(b'\) is two-thirds of the median from vertex B and \(b''\) is one-third of the median from vertex B. Using the median formula from vertex B and making the substitutions, we obtain:

(i) \(\frac{b^2}{4}+ \left ( \frac{2}{3}\frac{\sqrt{ 2a^2+2c^2-b^2}}{2} \right )^2 - \) \(\left ( \frac{1}{3}\frac{\sqrt{ 2a^2+2c^2-b^2}}{2} \right )^2 = c^2\)

(ii) \(\frac{b^2}{4}+\frac{2a^2+2c^2-b^2}{9}-\) \(\frac{2a^2+2c^2-b^2}{36}=c^2\)

(iii) \(\frac{9b^2}{36}+\frac{8a^2+8c^2-4b^2}{36}-\) \(\frac{2a^2+2c^2-b^2}{36}=c^2\)

(iv) \(6b^2+6a^2+6c^2=36c^2\)

(v) \(a^2+b^2=5c^2\)

The triangle ABC above in image is a √5, 3, 4 triangle. The shortest side is always side c.

The length of the median from vertex C is \(c_{m} =\frac{\sqrt{ 2a^2+2b^2-c^2}}{2}\). If the medians are perpendicular, then we know \(b^2 = 5c^2 - a^2\). Making this substitution into the median formula, we get: \(c_m=\frac{\sqrt{2a^2+2(5c^2-a^2)-c^2}}{2}\) \(= \frac{\sqrt{2a^2-2a^2+10c^2-c^2}}{2}\) \(= \frac{\sqrt{9c^2}}{2}=\frac{3c}{2}\). Therefore, if the medians are perpendicular, then the length of the longest median (the median from vertex C) is three-halves of c and the median is divided into lengths of c and c/2 by the point of concurrency O.

For any triangle that has perpendicular medians, triangles AOC' and BOC' are isosceles triangles, where AC' = C'O = C'B = c/2.

If ABC is an isosceles triange with CA = CB = a and the medians are perpendicular, then \(c^2 = \frac{2}{5}a^2\). And by law of cosines, we have \(c^2 = 2a^2 - 2a^2\cos C\) or \(c^2 = 2a^2(1 - \cos C)\).

Making the substitution for \(c^2\), we have \(\cos C = 1 - \frac{\frac{2}{5}a^2}{2a^2}=1-\frac{2}{10}=\frac{4}{5}\).

Therefore, there is one and only one isosceles triangle that has medians that are perpendicular, and its vertex angle C (the smallest angle) is given by arccos(4/5), which is approximately 36.87° or 0.64 radians. The equal angles A and B equal about 71.57°.

The trapezoid AB'A'B is an isosceles trapezoid. Since A'OB' and AOB are similar triangles because they are formed by the medians, the dimensioins of A'OB' are half of AOB. Therefore, OI is half of C'O. C'O is half of c as noted above. Therefore, OI = c/4.

The midpoints of AB' and A'B have been shown. The perpendicular bisectors of these two segments is the circumcenter of the isoscleles trapezoid. Moreover, AFDC' and BHDC' are both cyclic quadrilaterals because their opposite angles are 90 degrees. In the same way, B'FDI and KHDI are also both cyclic quadrilaterals. Actually, all 4 qudrilaterals are cyclic and are congruent. Also note that DB' and DB are equal since they are the radius of the circle D (and the diameter of the smaller circles). Therefore, BDB' is an isosceles triangle. Therefore, all 4 circles (in maroon) are congruent. That was expected since the quadrilaterals are also congruent.

Lastly, CD = CO = OI = c/4. Proof is simple. DB' and DA are equal since they are diameters of congruent circles. Also, BD and DA' are also equal since they are diameters of congruent circles. We can use this to prove that DIB' and BC'D are congruent right triangles. Since B'I is one-fourth of c, C'D is also one-fourth of c. Now AC' and C'O are equal as noted above. Therefore, DO has to be one-fourth of c also.

The radius of the bigger circle that circumscribes the trapezoid is \(\sqrt{\left ( \frac{c}{2} \right )^2+\left ( \frac{c}{4} \right )^2} = \frac{\sqrt{5}}{4}c\). The radius of the 4 smaller circles is half of that or \(\frac{\sqrt{5}}{8}c\).

Lastly, we focus on the segments DP and DN. Both are concurrent with the concurrency of the smaller circles. This can easily be shown, knowig that triangle BDB' is an isosclese triangle. Its sides that are equal in length are the diameters of the cirles. Therefore, triangles DNB' and DNB are both right triangles that divide BB' in half. Since the hypoteneus of these triangles is the diatemeter of the bigger circle, they have to be right triangles. Morever, since the altitudes (DN and DP) are perpendicular, this makes the quadrilateral DNOP a square!

To find the length of this segment (or the length of the side of this square), we need to know half the medium BB' and the diameter of the smaller circle. The length of BB' can be found using the median formula. First, side a can be represented by c since 2a² = c². Therefore, \(AA' = BB' = \frac{\sqrt{2(\frac{\sqrt{10}}{2}c)^2 + 2c^2 - (\frac{\sqrt{10}}{2}c)^2}}{2} =\) \( \frac{3\sqrt{2}}{4}c\). Half of that is BN. And the diameter BD is \(\frac{\sqrt{5}}{4}c\).

Using the Pythagorean Theorem, we have \(\textrm{DN} = \sqrt{\left ( \frac{\sqrt{5}}{4}c \right )^2 - \left ( \frac{3\sqrt{2}}{8}c \right )^2} = \) \( \sqrt{\frac{2}{64}c^2} = \frac{\sqrt{2}}{8}c\). Note that DO, the diagonal of the square, is c/4 Therefore, our length of the side of the square is confirmed.

Reader should note some other observations not explictely mentioned. For example, Point D is the concurrency point of all 4 smaller circles and it is also the center of the bigger circle!

Right Triangles

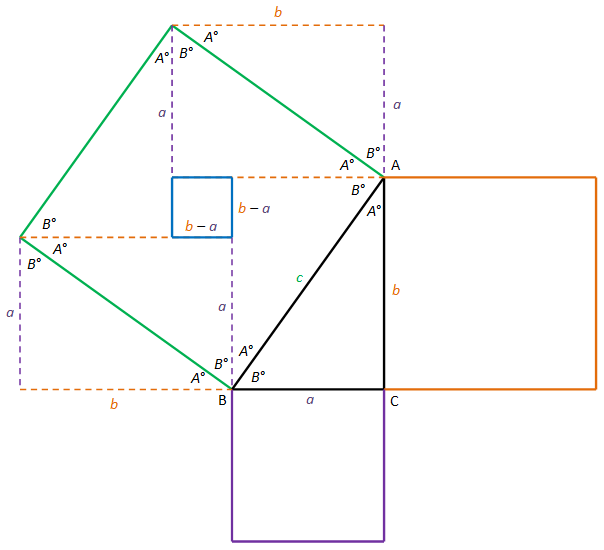
Right triangles are special triangles. One angle of a right triangle equals 90° making a perfect L shape. The other two angles are complementary angles, meaning that their sum equals 90°. In the Law of Cosines section above, we learned that, for a right triangle, c² = a² + b². This is not the proof of the Pythagorean theorem, however, as we relied on the Pythagorean theorem to derive the law of cosines. The Pythagorean theorem can be proved without using any trigonometry. The figure on the right shows how it can be proved with simple algebra, geometry, and area formulas.

Study the figure to determine how the angles and measure of the sides were identified. The complementary angles property of right triangles was used. Ultimately, a small square in the center (shown in blue) of the square on side c was derived and the measure of its sides is b - a. All we need to do is sum the area of the 4 triangles and the square. The area of 1 of the triangles is equal to the area of ΔABC, which is ½ab. So the area of all 4 triangles equal 2ab. The area of the small square equals (b - a)² = b² - 2ab + a². Hence, area of the square on side c equals c² = 2ab + b² - 2ab + a² = a² + b².