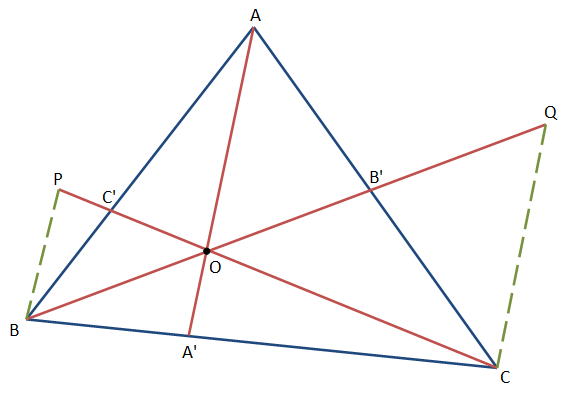
Ceva’s Theorem of Concurrency

Ceva’s Theorem: If three cevians, drawn from the vertices of a triangle are concurrent, then the following relationship holds true: \(\dfrac{AC'}{C'B}\cdot\dfrac{CB'}{B'A}\cdot\dfrac{BA'}{A'C}=1\).

We will prove the theorem above. However, the converse of this theorem is also true. The converse of the theorem states that if the above relationship is true, then the three lines must be concurrent. The converse is used to prove concurrency of three segments.

Triangle ABC is any arbitrary acute triangle. We draw segments BP and CQ (in red) such that these segments are parallel to segment AA'. We extend CC' to meet P and BB' to meet Q.

From similar triangles CA'O and CBP, we have: (a) \(\frac{CA'}{OA'}=\frac{BC}{BP}\). From similar triangles BA'O and BCQ, we have: (b) \(\frac{BA'}{OA'}=\frac{BC}{QC}\). Multiplying these results gives us:

(i) \(\dfrac{BA'}{A'C}=\dfrac{BP}{QC}\).

Now, from similar triangles BC'P and AC'O, we have the following equality: (c) \(\frac{C'B}{BP}=\frac{AC'}{AO}\). From similar triangles CB'Q and AB'O, we have: (d) \(\frac{CQ}{CB'}=\frac{AO}{B'A}\). We can multiply and rearrange these two to obtain:

(ii) \(\dfrac{AC'}{C'B}\cdot\dfrac{CB'}{B'A}=\dfrac{CQ}{BP}\).

Multiplying (i) and (ii), we obtain:

(iii) \(\dfrac{AC'}{C'B}\cdot\dfrac{CB'}{B'A}\cdot\dfrac{BA'}{A'C}=\dfrac{CQ}{BP}\cdot\dfrac{BP}{QC}=1\).

This completes the proof.