Multiple Angle Identities for Cosine and Sine
C o n c e p t s
This topic requires familiarity with the following concepts:
- Conic equations
- Differentiation
- Integration
- Rotating graphs
- Golden ratio
We know the identities for sin(2x) and cos(2x), but what about sin(nx) and cos(nx)? I have found a method to find the identities for cos(nx) and other properties relating sin(nx) and cos(nx) in the form of \(\sum_{i}^{ }a_i\cos ^i(x)\). First we find the identities for cos(3x) to cos(10x) exclusively in terms of cosx using the sum formula of cosine. They are listed here:
Table 1: Cosine Identities for n = 1 to 10
| cos(1x) | 1cos1x |
| cos(2x) | 2cos2x – 1 |
| cos(3x) | 4cos3x – 3cos1x |
| cos(4x) | 8cos4x – 8cos2x + 1 |
| cos(5x) | 16cos5x – 20cos3x + 5cos1x |
| cos(6x) | 32cos6x – 48cos4x + 18cos2x – 1 |
| cos(7x) | 64cos7x – 112cos5x + 56cos3x – 7cos1x |
| cos(8x) | 128cos8x – 256cos6x + 160cos4x – 32cos2x + 1 |
| cos(9x) | 256cos9x – 576cos7x + 432cos5x – 120cos3x + 9cos1x |
| cos(10x) | 512cos10x – 1280cos8x + 1120cos6x – 400cos4x + 50cos2x – 1 |
Notice that by increasing the n in cos(nx), the multiple of angle x, the number of terms increase, and we have a trigonometric polynomial each time. We’ll define a trigonometric polynomial as a polynomial containing either cosine or sine terms which have a 1 as the multiple of the angle x: \(\sum_{i}^{ }a_i\cos ^i(x)\). The trigonometric polynomial identities of cosine, where n is the multiple of angle x, have the following special characteristics:
- The coefficient of the term of the greatest degree is a power of 2.
- The signs alternate from positive to negative when the terms are arranged in decreasing degrees.
- The degrees of the terms decrease by 2. If the multiple is even, the degrees of all the terms are even. If the multiple is odd, the degrees of all the terms are odd.
- The greatest degree of the trigonometric polynomial identity is the multiple of angle x.
- The sum of the coefficients of the trigonometric polynomial identity is always 1. This can be proved easily by noting that cos(0) = 1.
We actually have a general formula for any n:
The multiple-angle identity of the cosine function is given by the formula:
\[\cos(nx) = \sum_{k=1}^{\left \lfloor \frac{n}{2} \right \rfloor +1} \frac{(-1)^{k-1} 2^{n+1-2k}\cdot n(n-k)!}{(k-1)!(n+2-2k)!}(\cos x)^{n+2-2k}\]
We will derive this formula later. However, first, we will do the manual calculation of finding the coefficients. Somehow, I found a method for generating the coefficients by accident. There’s no proof but it works!
First, write the odd numbers as the first row, denoted by \(R_1\), starting with 1:
\(R_1(n) = 2n-1\): 1 3 5 7 9 11 .....The sequence in Row 2, denoted by \(R_2\), is determined by the formula:
\(R_2(n) = 2\sum_{i=1}^{n} 2i-1\): 2 8 18 32 50 72 .....The sequence in Row 3 is determined by the formula:
\(R_3(n) = 4\sum_{i=1}^{n}\sum_{i_1=1}^{i} 2i_1-1\): 4 20 56 120 220 364The pattern is evident and the formula for Row 4 is:
\(R_4(n) = 8\sum_{i=1}^{n}\sum_{i_1=1}^{i}\sum_{i_2=1}^{i_1} 2i_2-1\): 8 48 160 400 840 1568 2688Continue this process to find as many rows as desired.
| Row 1: | 1 | 3 | 5 | 7 | 9 | 11 | ... |
| Row 2: | 2 | 8 | 18 | 32 | 50 | 72 | ... |
| Row 3: | 4 | 20 | 56 | 120 | 220 | 364 | ... |
| Row 4: | 8 | 48 | 160 | 400 | 840 | 1568 | ... |
| Row 5: | 16 | 112 | 432 | 1232 | 2912 | 6048 | ... |
| Row 6: | 32 | 256 | 1120 | 3584 | 9408 | 21504 | ... |
Column 1 contains coefficient of the highest degree terms. Column 2 contains coefficients of the next highest degree terms, and so on. But the columns after Column 1 have to be dropped down. Drop the columns down as shown below.
| Row 1: | 1 | 0 | 0 | 0 | 0 | 0 | ... |
| Row 2: | 2 | 1 | 0 | 0 | 0 | 0 | ... |
| Row 3: | 4 | 3 | 0 | 0 | 0 | 0 | ... |
| Row 4: | 8 | 8 | 1 | 0 | 0 | 0 | ... |
| Row 5: | 16 | 20 | 5 | 0 | 0 | 0 | ... |
| Row 6: | 32 | 48 | 18 | 1 | 0 | 0 | ... |
| Row 7: | 64 | 112 | 56 | 7 | 0 | 0 | ... |
| Row 8: | 128 | 256 | 160 | 32 | 1 | 0 | ... |
Column 2 should start with one 0 and a 1. Column 3 should start with three 0’s and a 1. Column 4 should start with five 0’s and a 1, and so on. Each time an odd number of 0’s are added and a 1 is added because for cos(2nx) where 2n is an even number, our trigonometric polynomial ends with a positive or a negative 1. The signs of the trigonometric polynomial can be determined easily because they alternate. Finally, the above table of rows and columns represent the coefficients of the trigonometric polynomial for cos(nx). (Row n represents the coefficients the trigonometric polynomial of cos(nx).) All these identities can be confirmed with a graphing utility.
We’ve only examined the identities for cos(nx). The identities of sin(nx) are unusual. Because sin(2x) equals 2sin x·cos x, sin(2nx) where 2n is even cannot be expressed exclusively in terms of sin x and they do not form a trigonometric polynomial according to our definition.
Table 2: Cosine and Sine Identities Comparison
| N | SIN(NX) | COS(NX) |
| 1 | \(\sin x\) | \(\cos x\) |
| 2 | \(\cos x(2\sin x)\) | \(2\cos^{2}x - 1 = \) \(1 - 2\sin^{2}x\) |
| 3 | \( 3\sin x - 4\sin^{3}x \) | \( 4\cos^{3}x - 3\cos x \) |
| 4 | \(2\sin(2x)\cos(2x) = \) \( \cos x(4\sin x - 8\sin^{3}x)\) | \(8\cos^{4}x - 8\cos^{2}x + 1 = \) \( 1 - 8\sin^{2}x + 8\sin^{4}x\) |
| 5 | \( 5\sin x - 20\sin^{3}x + 16\sin^{5}x \) | \( 16\cos^{5}x - 20\cos^{3}x + 5\cos x \) |
| 6 | \( 3\sin(2x) - 4\sin^{3}(2x) =\) \(\cos x(6\sin x - 32\sin^{3}x + 32\sin^{5}x)\) | \( 32\cos^{6}x - 48\cos^{4}x + 18\cos^{2}x - 1 = \) \( 1 - 18\sin^{2}x + 48\sin^{4}x - 32\sin^{6}x \) |
| 7 | \( 7\sin x - 56\sin^{3}x + \text{ }\) \( 112\sin^{5}x - 64\sin^{7}x \) | \( 64\cos^{7}x - 112\cos^{5}x + \) \( 56\cos^{3}x - 7\cos x \) |
| 8 | \(\cos x(8\sin x - 80\sin^{3}x + \) \( 192\sin^{5}x - 128\sin^7x)\) | \( 128\cos^{8}x - 256\cos^{6}x + \text{ }\) \( 160\cos^{4}x - 32\cos^{2}x + 1 \) |
| 9 | \( 9\sin x - 120\sin^{3}x + \) \( 432\sin^{5}x - 576\sin^{7}x - \) \( 256\sin^{9}x \) | \(256\cos^{9}x - 576\cos^{7}x + \) \( 432\cos^{5}x - 120\cos^{3}x + \) \( 9\cos x \) |
| 10 | \( \cos x (10\sin x - 160\sin^3 x + 672\sin^5 x \) \( - 1024\sin^7 x + 512\sin^9 x) \) | \( 512\cos^{10}x - 1280\cos^{8}x + \) \( 1120\cos^{6}x - 400\cos^{4}x \text{ } + \) \(50\cos^{2}x - 1 \) |
Notice that if you reverse the order and switch cosine with sine for the odd powers, we can the multiple-angle identity of the sine function.
There has to be a pattern for the even identities of sine but I have not investigated that yet. We can take the cosine out in the even identities of sine.
The Fibonacci Sequence
The Fibonacci sequence has a tendency to appear in the strangest places as it does in Pascal’s triangle. Our trigonometric polynomial is no exception for the Fibonacci sequence to appear. Let’s look at the coefficients of cos(nx) more closely.
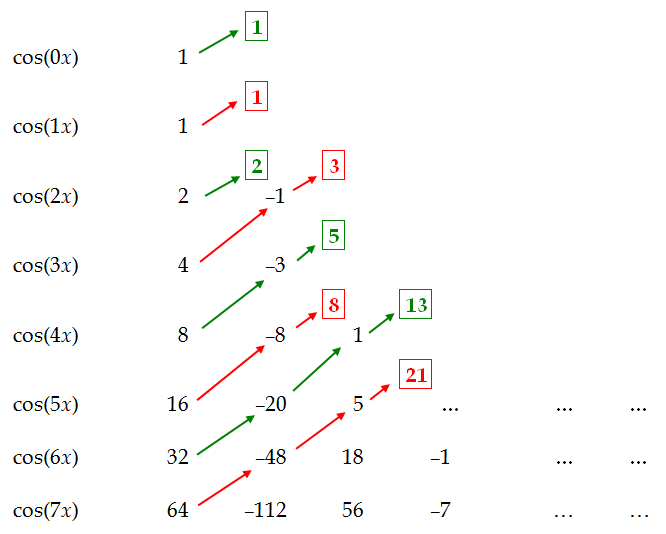
Add up the terms going diagonally from left to right to reveal the sequence: 1, 1, 2, 3, 5, 8, 13, 21....
Pattern of Squares
An interesting series appears when obtaining the derivatives of the identities and adding their coefficients.
| Derivative | Sum of Coefficients | |
| cos(1x) | –1sin1x | –1 |
| cos(2x) | –4cos1xsin1x | –4 |
| cos(3x) | –12cos2xsin1x + 3sin1x | –12 + 3 = –9 |
| cos(4x) | –32cos3xsin1x + 16cos1xsin1x | –32 + 16 = –16 |
| cos(5x) | –80cos4xsin1x + 60cos2xsin1x – 5sin1x | –80 + 60 – 5 = –25 |
| cos(6x) | –192cos5xsin1x + 192cos3xsin1x – 36cos1xsin1x | –192 + 192 – 36 = –36 |
| cos(7x) | –448cos6xsin1x + 560cos4xsin1x – 168cos2xsin1x + 7sin1x | –448 + 560 – 168 + 7 = –49 |
| cos(8x) | –1024cos7xsin1x + 1536cos5xsin1x – 640cos3xsin1x + 64cos1xsin1x | –1024 + 1536 – 640 + 64 = –64 |
| cos(9x) | –2304cos8xsin1x + 4032cos6xsin1x – 2160cos4xsin1x + 360cos2xsin1x – 9sin1x | –2304 + 4032 – 2160 + 360 – 9 = –81 |
| cos(10x) | –5120cos9xsin1x + 10240cos7xsin1x – 6720cos5xsin1x + 1600cos3xsin1x – 100cos1xsin1x | –5120 + 10240 – 6720 + 1600 = 100 = –100 |
We have a pattern of squares when adding the coefficients of the derivatives.
Proof of the General Trigonometric Polynomial Identity
The method for finding the identity of cos(nx) shown above is not practical for large values of n. There is a general formula for finding the coefficients of the identities. Here, I will reveal the general trigonometric polynomial identity for cos(nx) in a proof which only involves algebra.
Euler proved that \(e^{xi} = \cos(x) + i\sin(x)\), where i is the imaginary unit. Using this equation we will find the general identity for cos(nx).
\[(e^{xi})^{n} = (\cos(x) + i\sin(x))^{n}\]
Expanding \((\cos(x) + i\sin(x))^{n}\), we have:
(i) \((e^{xi})^{n} = (\cos(x) + i\sin(x))^{n} = \cos^{n}{x} + C_{1}^{n}(\cos{x})^{n-1}i\sin{x} + \) \(C_{2}^{n}(\cos{x})^{n-2}(i\sin{x})^{2} + C_{3}^{n}(\cos{x})^{n-3}(i\sin{x})^{3} + \) \(C_{4}^{n}(\cos{x})^{n-4}(i\sin{x})^{4} + ...\)
Now, group the real part from the imaginary part in expansion.
(ii) \(e^{nxi} = [\cos^{n}{x} - C_{2}^{n}(\cos{x})^{n-2}(\sin{x})^{2} + C_{4}^{n}(\cos{x})^{n-4}(\sin{x})^{4} - C_{6}^{n}(\cos{x})^{n-6}(\sin{x})^{6} + ...]\) \(+i[C_{1}^{n}(\cos{x})^{n-1}\sin{x} - C_{3}^{n}(\cos{x})^{n-3}(\sin{x})^{3} + C_{5}^{n}(\cos{x})^{n-5}(\sin{x})^{5} - C_{7}^{n}(\cos{x})^{n-7}(\sin{x})^{7} + ...]\)
But since \((e^{xi})^{n} = e^{nxi} = \cos{(nx)} + i\sin{(nx)}\), which equals the expansion above, the real part in the expansion must be cos(nx), and the imaginary part must be isin(nx). Therefore, we have the following identity of sine:
(1) \(\sin{(nx)} = C_{1}^{n}(\cos{x})^{n-1}\sin{x} - \) \(C_{3}^{n}(\cos{x})^{n-3}(\sin{x})^{3} +\) \( C_{5}^{n}(\cos{x})^{n-5}(\sin{x})^{5} -\)\( C_{7}^{n}(\cos{x})^{n-7}(\sin{x})^{7} ...\)
This expression is difficult to simplify but the next property for cosine is fairly easier:
(2) \(\cos{(nx)} = \cos^{n}{x} - C_{2}^{n}(\cos{x})^{n-2}(\sin{x})^{2} +\) \( C_{4}^{n}(\cos{x})^{n-4}(\sin{x})^{4} -\)\( C_{6}^{n}(\cos{x})^{n-6}(\sin{x})^{6} + ...\)
Because \(\cos^{2}{x} = 1 - \sin^{2}{x}\), we can substitute this in the above relationship to rewrite the relationship completely in terms of cosx.
(iii) \(\cos{(nx)} = \cos^{n}{x} - C_{2}^{n}(\cos{x})^{n-2}(1-\cos^{2}{x}) + \) \( C_{4}^{n}(\cos{x})^{n-4}(1-\cos^{2}{x})^{2} - \) \( C_{6}^{n}(\cos{x})^{n-6}(1-\cos^{2}{x})^{3} + ...\)
(iv) \(\cos{(nx)} = \cos^{n}{x} - C_{2}^{n}[(\cos{x})^{n-2} - \cos^{n}{x}] + \) \(C_{4}^{n}[(\cos{x})^{n-4} - C_{1}^{2}\cos{x}^{n-2} + \cos^{n}{x}] - \) \( C_{6}^{n}[(\cos{x})^{n-6} - C_{1}^{3}(\cos{x})^{n-4} + C_{2}^{3}(\cos{x})^{n-2} - C_{3}^{3}(\cos{x})^{n}] + \) \( C_{8}^{n}[(\cos{x})^{n-8} - C_{1}^{4}(\cos{x})^{n-6} + C_{2}^{4}(\cos{x})^{n-4} - C_{3}^{4}(\cos{x})^{n-2} + C_{4}^{4}(\cos{x})^{n}]...\)
Collecting the like terms gives us the following Cosine Identity:
(v) \(\cos{(nx)} = [1 + C_{2}^{n} + C_{4}^{n} + C_{6}^{n} + C_{8}^{n} + ....]\cos^{n}(x) - \)\( [C_{2}^{n}C_{0}^{1} + C_{4}^{n}C_{1}^{2} + C_{6}^{n}C_{2}^{3} + C_{8}^{n}C_{3}^{4} + ...]\cos{x}^{n-2} + \)\( [C_{4}^{n}C_{0}^{2} + C_{6}^{n}C_{1}^{3} + C_{8}^{n}C_{2}^{4} + C_{10}^{n}C_{3}^{5} + ...]\cos{x}^{n-4} - \)\( [C_{6}^{n}C_{0}^{3} + C_{8}^{n}C_{1}^{4} + C_{10}^{n}C_{2}^{5} + C_{12}^{n}C_{3}^{6} + ...]\cos{x}^{n-6} + ...\)
From (v), we have this nice multiple angle identity for cosine.
\(\displaystyle \cos{(nx)}=\left (\sum_{i=0}^{\left \lfloor \frac{n}{2} \right \rfloor+1}C_{2i}^n \right )(\cos{x})^{n} - \) \(\displaystyle \left (\sum_{i=1}^{\left \lfloor \frac{n}{2} \right \rfloor}C_{2i}^n\cdot C_{i-1}^{i} \right )(\cos{x})^{n-2} + \) \(\displaystyle \left (\sum_{i=2}^{\left \lfloor \frac{n}{2} \right \rfloor - 1}C_{2i}^n\cdot C_{i-2}^{i} \right )(\cos{x})^{n-4} - \) \(\displaystyle \left (\sum_{i=3}^{\left \lfloor \frac{n}{2} \right \rfloor - 2}C_{2i}^n\cdot C_{i-3}^{i} \right )(\cos{x})^{n-6} + \) \(\displaystyle \left (\sum_{i=4}^{\left \lfloor \frac{n}{2} \right \rfloor - 3}C_{2i}^n\cdot C_{i-4}^{i} \right )(\cos{x})^{n-8} - \) \(\displaystyle \left (\sum_{i=5}^{\left \lfloor \frac{n}{2} \right \rfloor - 4}C_{2i}^n\cdot C_{i-5}^{i} \right )(\cos{x})^{n-10} + ...\), where \(\left \lfloor \frac{n}{2} \right \rfloor\) is the floor function.
The first 5 coefficients for any n can be reduced to the following general formulas:
(1) \(\sum_{i = 0}^{\left \lfloor \frac{n}{2} \right \rfloor + 1 }C_{2i}^{n}=2^{n-1}\), where n ≥ 0
(2)\(\sum_{i = 1}^{\left \lfloor \frac{n}{2} \right \rfloor }C_{2i}^{n}\cdot C_{i-1}^{i}=2^{n-3}(n) = \frac{2^{n-3}}{1!}(n)\), where n ≥ 2
(3)\(\sum_{i = 2}^{\left \lfloor \frac{n}{2} \right \rfloor - 1}C_{2i}^{n}\cdot C_{i-2}^{i}=2^{n-6}(n)(n-3) = \frac{2^{n-5}}{2!}(n)(n-3)\), where n ≥ 4
(4)\(\sum_{i=3}^{\left \lfloor \frac{n}{2} \right \rfloor - 2}C_{2i}^{n}\cdot C_{i-3}^{i} =\) \( 2^{n-6}\left [ \frac{7}{2} + \frac{9}{2}(n-7) + \frac{5}{4}(n-7)(n-8) + \frac{1}{12}(n-7)(n-8)(n-9) \right ] = \) \( 2^{n-6}\left ( \frac{1}{12} \right )(n)(n-4)(n-5) = \)\( 2^{n-8}(1/3)(n)(n-4)(n-5) = \)\( \frac{2^{n-7}}{3!}(n)(n-4)(n-5)\), where n ≥ 6
(5)\(\sum_{i=4}^{\left \lfloor \frac{n}{2} \right \rfloor - 3}C_{2i}^{n}\cdot C_{i-4}^{i} = \) \( 2^{n-12}\left ( \frac{1}{3} \right )(n)(n-5)(n-6)(n-7) = \) \( \frac{2^{n-9}}{4!}(n)(n-5)(n-6)(n-7)\), where n ≥ 8
However, it seems finding the general formula for other powers seems more and more complex when done manually. I have shown how to derive the formula for the 6th term below. However, a pattern does seem to emerge (hence I’ve written the formulas above with the factorials to see if a pattern emerges.) Assuming this pattern is correct, let’s write the formula for coefficient of the 6th term:
(6)\(\sum_{i=5}^{\left \lfloor \frac{n}{2} \right \rfloor - 4}C_{2i}^{n}\cdot C_{i-5}^{i} = \frac{2^{n-11}}{5!}(n)(n-6)(n-7)(n-8)(n-9)\), where n ≥ 10
Does this formula check for the \((\cos x)^{n-10}\) term? Let’s compute the coefficients starting with n = 10.
(i) \(\frac{2^{10-11}}{5!}(10)(10-6)(10-7)(10-8)(10-9) = \)\( \frac{2^{-1}}{5\cdot 4!}(10)(4)(3)(2)(1)=1\)
So far so good. I’ll skips the in-between steps going forward.
(ii) \(\frac{2^{0}}{5!}(11)(5)(4)(3)(2) = 11\)
Works again. Let’s continue with n = 12.
(iii) \(\frac{2^{1}}{5!}(12)(6)(5)(4)(3) = 72\)
Doing great so far. And now, n = 13.
(iv) \(\frac{2^{2}}{5!}(13)(7)(6)(5)(4) = 364\)
Amazing! The pattern holds up. This is not a rigorous proof required by mathematics. I’ll leave that up to others to figure that out.
Manual Calculation for cos(10x)
This is a manual calulation example for the coefficents of \(\cos^{10}x\). The coefficients are:
\(C_{0}^{10}+C_{2}^{10}+C_{4}^{10}+C_{6}^{10}+C_{8}^{10}+C_{10}^{10} = \)\(1 + 45 + 210 + 210 + 45 + 1 = 512\)
For the cos8x coefficient:
\(C_{2}^{10}C_{0}^{1} + C_{4}^{10}C_{1}^{2} + \) \( C_{6}^{10}C_{2}^{3} + C_{8}^{10}C_{3}^{4}+C_{10}^{10}C_{4}^{5} = \) \( 45\cdot1 + 210\cdot2 + 210\cdot3 + 45\cdot4 + 1\cdot5 = 45 + 420 + 630 + 180 +5 = 1280\)
For the cos6x coefficient:
\(C_{4}^{10}C_{0}^{2} + C_{6}^{10}C_{1}^{3} + \) \( C_{8}^{10}C_{2}^{4} + C_{10}^{10}C_{3}^{5} = \) \(210\cdot1 + 210\cdot3 + 45\cdot6 + 1\cdot10 = 210 + 630 + 270 + 10 = 1120\)
For the cos4x coefficient:
\(C_{6}^{10}C_{0}^{3} + C_{8}^{1}0C_{1}^{4} + C_{10}^{10}C_{2}^{5} = \) \(210\cdot1 + 45\cdot4 + 1\cdot10 = \) \(210 + 180 + 10 = 400\)
For the cos2x coefficient:
\(C_{8}^{10}C_{0}^{4} + C_{10}^{10}C_{1}^{5} = \) \( 45\cdot1 + 1\cdot5 = 45 + 5 = 50\)
For the cos0x (the constant):
\(C_{10}^{10}C_{0}^{5} = 1\cdot1 = 1\)
So, our formula for \(\cos^{10}x\) is:
\(\cos^{10}x = 512\cos^{10}x - 1280\cos^{8}x \text{ } + \) \( 1120\cos^{6}x - 400\cos^{4}x \text{ } + \) \(50\cos^{2}x - 1\).
The General Formula for the Coefficients
From the pattern above, we can put the coefficients into a formula for any n. The pattern fits the formula here:
The coefficients of the multiple-angle identities of the cosine function are given by the formula:
\[ \frac{2^{n+1-2k}\cdot n(n-k)!}{(k-1)!(n+2-2k)!} \]
where the sign alternates and k is the kth term of for the nth multiple of cosine.
Therefore, the cosine identity in one formula is:
The multiple-angle identity of the cosine function is given by the formula:
\[\cos(nx) = \sum_{k=1}^{\left \lfloor \frac{n}{2} \right \rfloor +1} \frac{(-1)^{k-1} 2^{n+1-2k}\cdot n(n-k)!}{(k-1)!(n+2-2k)!}(\cos x)^{n+2-2k}\]
Let’s see if the formula works for n = 12, a number we haven’t tried before.
(i) \(\cos(nx) = \displaystyle \sum_{k=1}^{\left \lfloor \frac{n}{2} \right \rfloor +1} \frac{(-1)^{k-1} 2^{n+1-2k}\cdot n(n-k)!}{(k-1)!(n+2-2k)!}(\cos x)^{n+2-2k}\)
(ii) \(\cos(12x) = \displaystyle \sum_{k=1}^{\left \lfloor \frac{12}{2} \right \rfloor +1} \frac{(-1)^{k-1} 2^{12+1-2k}\cdot 12(12-k)!}{(k-1)!(12+2-2k)!}(\cos x)^{12+2-2k}\)
(iii) \(\cos(12x) = \displaystyle \sum_{k=1}^{7} \frac{(-1)^{k-1} 2^{13-2k}\cdot 12(12-k)!}{(k-1)!(14-2k)!}(\cos x)^{14-2k}\)
(iv) \(\cos(12x) = \dfrac{2^{11}\cdot 12(11)!}{(0)!(12)!}\cos^{12}x - \)\(\dfrac{2^{9}\cdot 12(10)!}{(1)!(10)!}\cos^{10}x +\)\( \dfrac{2^{7}\cdot 12(9)!}{(2)!(8)!}\cos^{8}x - \)\(\dfrac{2^{5}\cdot 12(8)!}{(3)!(6)!}\cos^{6}x +\)\( \dfrac{2^{3}\cdot 12(7)!}{(4)!(4)!}\cos^{4}x -\)\( \dfrac{2^{1}\cdot 12(6)!}{(5)!(2)!}\cos^{2}x + \)\(\dfrac{2^{-1}\cdot 12(5)!}{(6)!(0)!}\cos^{0}x \)
(v) \(\cos(12x) = 2^{11}\cos^{12}x - (2^9\cdot 12)\cos^{10}x + \text{ } \) \( (2^7\cdot 54)\cos^{8}x - (2^5\cdot 112)\cos^{6}x + \text{ }\)\( (2^3\cdot 105)\cos^{4}x - (2\cdot36)\cos^{2}x + (\frac{1}{2}\cdot 2)\cos^{0}x \)
(vi) \(\cos(12x) = 2048\cos^{12}x - 6144\cos^{10}x + \text{ } \) \( 6912\cos^{8}x - 3584\cos^{6}x + \text{ }\)\( 840\cos^{4}x - 72\cos^{2}x + 1 \)
\(\displaystyle \cos(12x) = 2048\cos^{12}x - 6144\cos^{10}x + \text{ } \) \(\displaystyle 6912\cos^{8}x - 3584\cos^{6}x + \text{ }\)\(\displaystyle 840\cos^{4}x - 72\cos^{2}x + 1 \)
Does it validate? Let’s try an obscure number... say 0.7. So, we have \(\cos(12\cdot 0.7) = \cos(8.4) \approx -0.5192887\).
And the result by wolfram: Result verifies.

 Conic Sections
Conic Sections