Deriving the Area of a Triangle Formula
One of the most famous formulas for triangles is the formula for the area of a triangle based on the sides of the triangle. Given any 3 lengths, there can only be 1 triangle that can be formed. This means that there exists a formula for the triangle in term of the sides, giving a unique area. I discovered a method for deriving formula for the area of a triangle based on the sides of a triangle using the perpendicular bisectors. At first, I thought it was a new formula. However, it turns out to be the same as Heron's formula when Heron's formula is simplified.
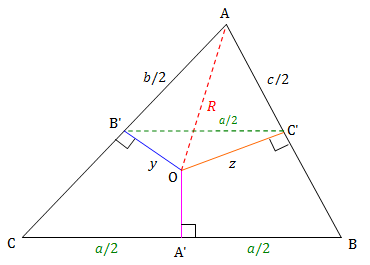
We have a triangle whose perpendicular bisectors meet at the common point O. The length of the bisectors from O to the sides of the triangle, OA', OB', and OC', are given as x, y, and z, respectively. We can use this triangle to find the area of the triangle in terms of the sides of the triangle.
Triangles AB'O and AC'O are both right triangles. Thus, the quadrilateral AB'OC' is a cyclic quadrilateral. It is easy to see why the length of B'C' = a/2 (it is a side of the medial triangle). The segment AO is the radius of the circumcircle of triangle ΔABC. From the relationship of the cyclic quadrilateral, we have the following:
(i) $R\cdot \frac{a}{2}=z\cdot \frac{b}{2}+y\cdot \frac{c}{2}$ or $aR=bz+cy$
However, we have the following relationships from the right triangles:
(ii) $y^2=R^2-\left (\frac{b}{2}\right)^2$ and $z^2=R^2-\left(\frac{c}{2}\right)^2$
Combining (i) and (ii), we obtain:
(iii) $aR=b\sqrt{R^2-\left(\frac{c}{2}\right)^2}+$ $c\sqrt{R^2-\left(\frac{b}{2}\right)^2}$
(iv) $a^2R^2-2acR\sqrt{R^2-\left(\frac{b}{2}\right)^2}+c^2R^2-\frac{c^2b^2}{4}=$ $b^2R^2-\frac{c^2b^2}{4}$ Squaring both sides.
The relationship in (iv) can be manipulated to obtain:
(v)$2ac\sqrt{R^2-\left(\frac{b}{2}\right)^2}=R(a^2+c^2+b^2)$
Solving for R in equation (v):
(vi)$R=\frac{abc}{\sqrt{2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4)}}$
We know that R is also given by the formula: $R=\frac{abc}{4K}$, where K is the area of the triangle. Thus, the area of the triangle can also be expressed as:
(vii)$4K=\sqrt{2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4)}$
We also know that $(a^2+b^2+c^2)^2=$ $a^4+b^4+c^4-2(a^2b^2+b^2c^2+c^2a^2)$. Thus, (vii) can be rewritten into the following elegant formula for the area of a triangle in terms of the sides:
(viii)$4K=\sqrt{(a^2+b^2+c^2)^2-2(a^4+b^4+c^4)}$

 Conic Sections
Conic Sections