Concurrency of Bisector Segments
Introduction
We know that the equiangular segments are concurrent and at the point of concurrency, they create angles of equal measure or 60˚. But the equiangular segments are actually a part of a whole set of concurrent lines that result from the perpendicular bisectors of a triangle. This allows us to state a theorem:
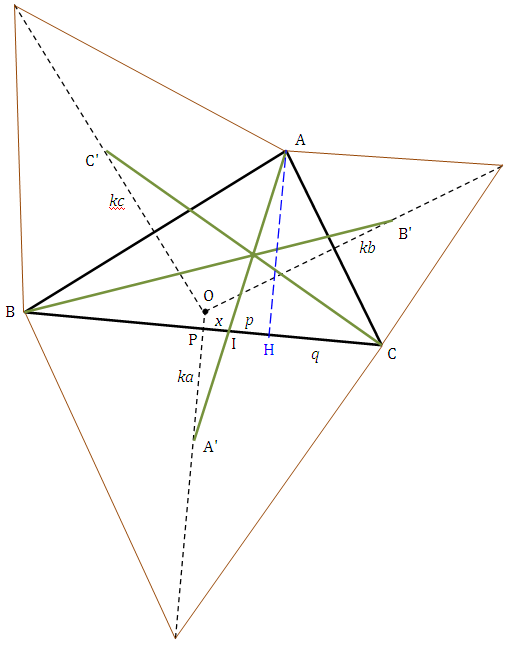
Theorem: Draw the perpendicular bisectors of the three sides of the triangle (shown in blue). Then draw points that are proportionally equidistant from the sides of the triangle on the perpendicular bisectors (A', B', and C'). Then connect the vertices to these points on the perpendicular bisectors. These segments are concurrent.
We have already proved the concurrency of the equiangular segments here. Now, we will prove the theorem above.
I will refer to these segments as bisector segments. Equiangular segments are then the special bisector segments which have one end fall on the equilateral triangle and create the 60˚ angles as mentioned above. Equiangular segments are discussed here.
In the drawing, point A', B', and C' were drawn on the perpendicular bisectors of triangle ABC. These points are proportionally equidistant from the sides of ΔABC, meaning that if the distance of A' from side BC is ka, then distance of B' and C' from sides CA and AB is kb and kc, respectively. Points A and A', B and B', and C and C' are connected. The segments AA', BB', and CC' are concurrent.
To prove the concurrency, altitude of side BC has been drawn (shown in blue).
x = PI = segment from perpendicular bisector to the segment AA'
p = IH = segment from AA' to altitude
q = HC = segment from altitude to vertex C
Let y and z be the counterparts of x on sides CA and AB.
Proof of Concurrency
By using the Pythagorean theorem, we can find q to be:
(i) $q=\frac{{{b}^{2}}+{{a}^{2}}-{{c}^{2}}}{2a}$
The proof of (i) is left to the reader.
Using the similar right triangles formed by the perpendicular bisector and altitude, the following proportion is true:
(ii) $\frac{ka}{{{h}_{\text{A}}}}=\frac{x}{p}$, where hA is the altitude of side BC
We also know that a/2 = x + p + q. Thus, we can find the value of x to be:
(iii) $x=\frac{k({{c}^{2}}-{{b}^{2}})}{2{{h}_{\text{A}}}+2ka}$, where hA is the altitude of side BC
Using the same method, we can find y and z, which would be on the sides CA and AB of the triangle:
(iv) $y=\frac{k({{a}^{2}}-{{c}^{2}})}{2{{h}_{\text{B}}}+2kb}$, where hB is the altitude of side CA.
(v) $z=\frac{k({{a}^{2}}-{{b}^{2}})}{2{{h}_{\text{C}}}+2kc}$, where hC is the altitude of side AB.
Now, we can prove the concurrency of the segment using Ceva’s theorem. We must prove that: $\frac{\left( \frac{1}{2}a+x \right)\left( \frac{1}{2}b+y \right)\left( \frac{1}{2}c+z \right)}{\left( \frac{1}{2}a-x \right)\left( \frac{1}{2}b-y \right)\left( \frac{1}{2}c-z \right)}=1$ or $\frac{(a+2x)(b+2y)(c+2z)}{(a-2x)(b-2y)(c-2z)}=1$. We can work with this expression individually and find the following simplification:
(vi) $\frac{a+2x}{a-2x}=\frac{{{h}_{\text{A}}}a+k({{a}^{2}}+{{c}^{2}}-{{b}^{2}})}{{{h}_{\text{A}}}a+k({{b}^{2}}+{{a}^{2}}-{{c}^{2}})}$
(vii) $\frac{b+2y}{b-2y}=\frac{{{h}_{\text{B}}}b+k({{a}^{2}}+{{b}^{2}}-{{c}^{2}})}{{{h}_{\text{B}}}b+k({{b}^{2}}+{{c}^{2}}-{{a}^{2}})}$
(viii) $\frac{c+2z}{c-2z}=\frac{{{h}_{\text{C}}}c+k({{b}^{2}}+{{c}^{2}}-{{a}^{2}})}{{{h}_{\text{C}}}c+k({{a}^{2}}+{{c}^{2}}-{{b}^{2}})}$
Note that hAa = hBb = hCc = 2S, where S is the area of the triangle. Thus, when we multiply (vi), (vii), and (viii), we obtain:
(ix) $\frac{2S+k({{a}^{2}}+{{c}^{2}}-{{b}^{2}})}{2S+k({{b}^{2}}+{{a}^{2}}-{{c}^{2}})}\cdot$ $ \frac{2S+k({{a}^{2}}+{{b}^{2}}-{{c}^{2}})}{2S+k({{b}^{2}}+{{c}^{2}}-{{a}^{2}})}\cdot$ $ \frac{2S+k({{b}^{2}}+{{c}^{2}}-{{a}^{2}})}{2S+k({{a}^{2}}+{{c}^{2}}-{{b}^{2}})}=1$
This completes the proof. We can see why the bisector segments are concurrent, which is a case where k = 1 and the points A', B', and C' are at the vertices of the equilateral triangles. Moreover, when k = 0, points A', B', and C' fall on the sides of the triangle and are the midpoints of the sides. We know that the midpoints are concurrent.
When k is negative, the points begin to fall inside the circle. Even when k is negative, the segments are concurrent.
In conclusion, the perpendicular bisectors contain a whole locus of points such that points proportionally equidistant from the sides of the triangle gives a locus of segments that are concurrent.
Length of the Bisector Segments
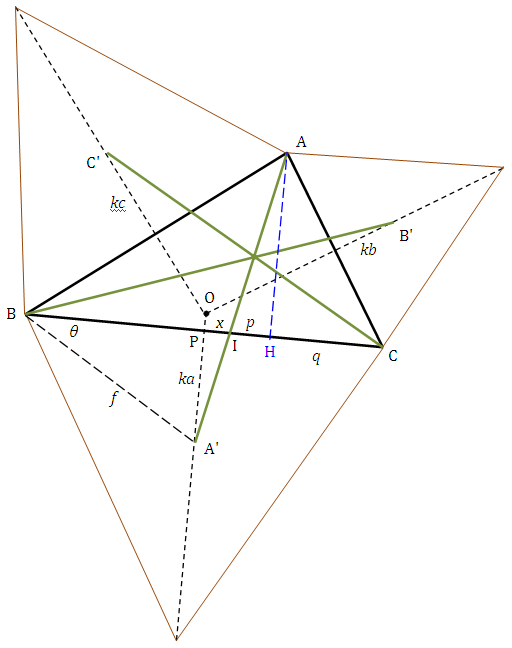
We can find the length of AA' by using the Law of Cosines. The length of AA' will enable us to tie the medians with the equiangular segments. In the figure on the right, triangle ABA' will enable us to find the length of AA', expresses as eA.
Let CA' = f. Let AA' = eA. Using the Law of Cosines, we have:
(i) $e_{\text{A}}^{2}={{f}^{2}}+{{c}^{2}}-2fc\cdot \cos (\theta +B)$
(ii) $e_{\text{A}}^{2}={{f}^{2}}+{{c}^{2}}-$ $2fc[\cos \theta \cos B-\sin \theta \sin B]$
The length of f can be determined by the Pythagorean Theorem: ${{f}^{2}}=\frac{{{a}^{2}}}{4}+{{k}^{2}}{{a}^{2}}$. Also sine and cosine of θ can easily be determined from the triangle PCA': $\cos \theta =\frac{1}{\sqrt{1+4{{k}^{2}}}}$ and $\sin \theta =\frac{2k}{\sqrt{1+4{{k}^{2}}}}$. This gives:
(iii) $e_{\text{A}}^{2}={{k}^{2}}{{a}^{2}}+\frac{{{a}^{2}}}{4}+{{c}^{2}}-$ $ac[\cos B-2k\cdot \sin B]$
Law of Cosines gives $\cos B=\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}$ and the area of a triangle formula gives $\sin B=\frac{2S}{ac}$, where S is the area of the triangle ABC.
(iv) $e_{\text{A}}^{2}={{k}^{2}}{{a}^{2}}+\frac{{{a}^{2}}}{4}+{{c}^{2}}-$ $ac\left[ \frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}-2k\cdot \frac{2S}{ac} \right]$
(v) $e_{\text{A}}^{2}={{k}^{2}}{{a}^{2}}-\frac{{{a}^{2}}}{4}+\frac{{{b}^{2}}}{2}+\frac{{{c}^{2}}}{2}+4kS$
The equation in (v) gives us the length of eA in terms of the sides of the triangle. Now, let’s verify with the two special points where A' falls on the side of the triangle and A' falls on the vertex of the equilateral triangle. When A' falls on the triangle, k = 0. This would give us the length of the medians.
(vi) $e_{\text{A}}^{2}=\frac{{{b}^{2}}}{2}+\frac{{{c}^{2}}}{2}-\frac{{{a}^{2}}}{4}=$ $\frac{2{{b}^{2}}+2{{c}^{2}}-{{a}^{2}}}{4}=m_{\text{A}}^{2}$
And formula (vi) checks with the formula for the length of median, mA, to side A.
When $k=\frac{\sqrt{3}}{2}a$, A' falls on the vertex of the equilateral triangle. Substituting this in (v) gives:
(vii) $ e_{\text{A}}^{2}=\frac{3}{4}{{a}^{2}}-\frac{{{a}^{2}}}{4}+\frac{{{b}^{2}}}{2}+\frac{{{c}^{2}}}{2}+3S=$ $\frac{1}{2}({{a}^{2}}+{{b}^{2}}+{{c}^{2}})+3S$
This is indeed the length for equiangular segments.
Equal Length Segments
We know that the three equiangular segments are equal in length. We wonder when else along the bisectors they are equal. To determine this, we let $e_{\text{A}}^{2}=e_{\text{B}}^{2}$.
(viii) ${{k}^{2}}{{a}^{2}}-\frac{{{a}^{2}}}{4}+\frac{{{b}^{2}}}{2}+\frac{{{c}^{2}}}{2}+4kS=$ ${{k}^{2}}{{b}^{2}}-\frac{{{b}^{2}}}{4}+\frac{{{a}^{2}}}{2}+\frac{{{c}^{2}}}{2}+4kS$
(ix) ${{k}^{2}}({{a}^{2}}-{{b}^{2}})-\frac{{{a}^{2}}}{4}+\frac{{{b}^{2}}}{2}=-\frac{{{b}^{2}}}{4}+\frac{{{a}^{2}}}{2}$
(x) ${{k}^{2}}=\frac{3}{4}$ or $k=\pm \frac{\sqrt{3}}{2}$
Hence, there are only two A' when the segments are equal in length. The first is when $k=\frac{\sqrt{3}}{2}$ and A' is the vertex of the equilateral triangles erected externally to the sides of ABC. The second is when $k=-\frac{\sqrt{3}}{2}$ where A' is on the vertex of the equilateral triangles erected internally to the sides of ABC. We knew both of these facts from Equiangular Segments discussion already!

 Conic Sections
Conic Sections