Menelaus’s Theorem of Collinearity

Menelaus’s Theorem: If three points (L, M, and N) are collinear (meaning that they lie on the same line), then the following relationship holds true: \( {\color{red} \frac{AL}{LC}\cdot\frac{BM}{MA}\cdot\frac{CN}{NB}=1} \).

Proof

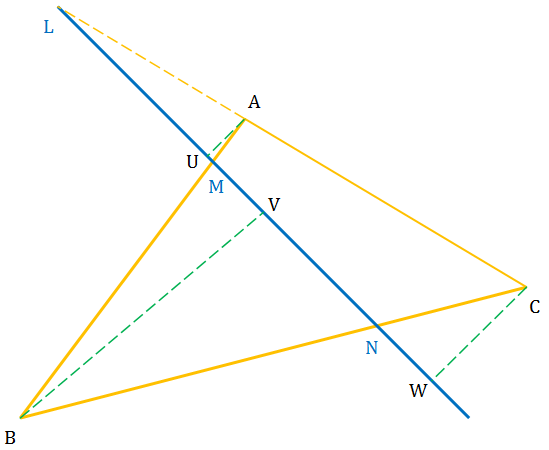Menelaus's Theorem To prove Menelaus’s Theorem, we draw perpendicular lines from the vertices of ΔABC to the line LN. From the similar triangles ΔALU and ΔCLW, we have the following relationship:

(i) \( {\color{red}\frac{AL}{-CL} = \frac{AL}{LC} = -\frac{AU}{CW}} \)

From the similar triangles ΔWCN and ΔVBN, we have the following relationship:

(ii) \( {\color{red}\frac{CN}{-BN} = \frac{CN}{NB} = -\frac{CW}{BV} } \)

From similar triangles ΔVBM and ΔUAN, we have the following relationship:

(iii) \( {\color{red}\frac{BM}{-AM} = \frac{BM}{MA} = -\frac{BV}{AU} } \)

Multiplying (i), (ii), and (iii), we obtain:

(iv) \( {\color{red} \frac{AL}{LC} \cdot \frac{BM}{MA} \cdot \frac{CN}{NB} \, =} \) \( {\color{red} -\frac{AU}{CW}\cdot - \frac{CW}{BV}\cdot - \frac{BV}{AU}= -1 } \)

The negative sign is necessary when considering the order of writing the segment. For example, segment LC = –CL.

This completes the proof. The converse of this theorem is also true. If the relations (iv) is true, then point L, M, and N must be collinear.